bzoj4144 [AMPPZ2014]Petrol

最新推荐文章于 2019-02-11 13:19:00 发布

转载最新推荐文章于 2019-02-11 13:19:00 发布 · 63 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/aziint/p/8481500.html

本文介绍了一种基于图论的问题解决方法，通过重新构建图结构，利用多源最短路径和最小生成树来判断两点间是否可达。适用于给定带有加油站的加权无向图，求解特定条件下两加油站间是否能通行。

Description

给定一个 $n$ 个点、 $m$ 条边的带权无向图，其中有 $s$ 个点是加油站。

每辆车都有一个油量上限 $b$ ，即每次行走距离不能超过 $b$ ，但在加油站可以补满。

$q$ 次询问，每次给出 $x,y,b$ ，表示出发点是 $x$ ，终点是 $y$ ，油量上限为 $b$ ，且保证 $x$ 点和 $y$ 点都是加油站，请回答能否从 $x$ 走到 $y$ 。

Input

第一行包含三个正整数 $n,s,m(2\le s\le n\le 200000,1\le m\le 200000)$ ，表示点数、加油站数和边数。

第二行包含 $s$ 个互不相同的正整数 $c[1],c[2],\cdots c[s] (1\le c[i]\le n) $ ，表示每个加油站。

接下来 $m$ 行，每行三个正整数 $u[i],v[i],d[i](1\le u[i],v[i]\le n,u[i]\ne v[i],1\le d[i]\le 10000)$ ，表示 $u[i]$ 和 $v[i]$ 之间有一条长度为 $d[i]$ 的双向边。

接下来一行包含一个正整数 $q(1\le q\le 200000)$ ，表示询问数。

接下来 $q$ 行，每行包含三个正整数 $x[i],y[i],b[i](1\le x[i],y[i]\le n,x[i]\ne y[i],1<\le b[i]\le 2\times 10^9)$ ，表示一个询问。

Output

输出 $q$ 行。第 $i$ 行输出第i个询问的答案，如果可行，则输出 $\mathrm{TAK}$ ，否则输出 $\mathrm{NIE}$ 。

Sample

Sample Input

Sample Output

TAK
TAK
TAK
NIE

Solution

真是一道结论诡好题。

大家肯定知道，不是加油站的点是废点。那加油站点该怎么重新建图呢？

来看一个图。红点表示加油站，黑点是废点。

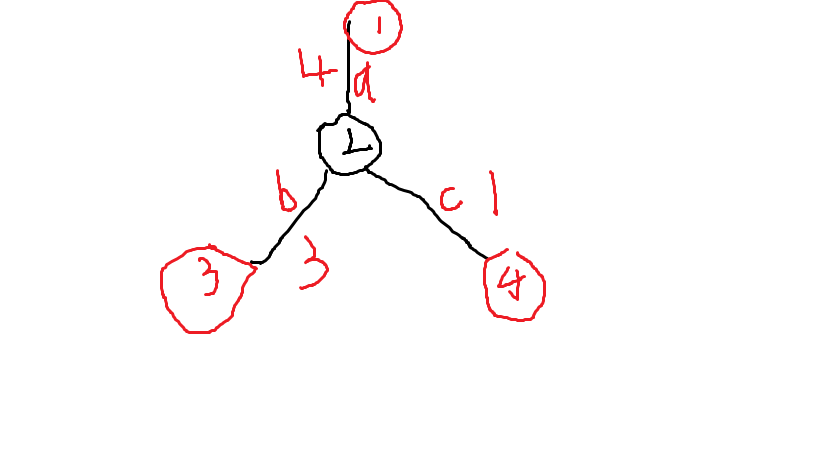
从 $1$ 到 $3$ 走简单路径会至少需要 $7$ 的油量，而从 $1$ 到 $4$ 再到 $3$ 则只需要准备 $5$ 的油量就可以了。这是因为 \[c<a 且 c<b \] 所以 \[c+b<a+b 且c+a<b+a\] 于是我们就得到了结论

从当前节点到最近的加油站再到其它的加油站不会更差

那么就可以多源最短路，最小生成树判断连通性就可以了。

具体细节见代码。

#include<bits/stdc++.h>
using namespace std;

#define N 400011
#define rep(i, a, b) for (int i = a; i <= b; i++)

inline int read() {
    int x = 0, flag = 1; char ch = getchar(); while (!isdigit(ch)) { if (!(ch ^ '-')) flag = -1; ch = getchar(); }
    while (isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar(); return x * flag;
}

int n, s, m, C[N], head[N], tot = 1, cnt, dis[N], near[N], fa[N];
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
queue<int> q;
bool inq[N], ans[N];
struct edge { int v, w, next; }e[N];
inline void add(int u, int v, int w) { e[++tot].v = v, e[tot].w = w, e[tot].next = head[u], head[u] = tot; }
struct edgeData {
    int u, v, w;
    edgeData(int _u = 0, int _v = 0, int _w = 0):u(_u), v(_v), w(_w) {}
    bool operator < (const edgeData& b) const { return w < b.w; }
}edt[N];
struct query {
    int id, S, T, d;
    bool operator < (const query& b) const { return d < b.d; }
}qu[N];
void spfa() {
    rep(i, 1, n) dis[i] = 0x7fffffff;
    rep(i, 1, s) q.push(C[i]), inq[C[i]] = 1, dis[C[i]] = 0, near[C[i]] = C[i];
    while (!q.empty()) {
        int u = q.front(); q.pop(), inq[u] = 0;
        for (int i = head[u], v; i; i = e[i].next) if (dis[v = e[i].v] > dis[u] + e[i].w) {
            dis[v] = dis[u] + e[i].w, near[v] = near[u];
            if (!inq[v]) q.push(v), inq[v] = 1;
        }
    }
    rep(u, 1, n) for (int i = head[u], v; i; i = e[i].next) if (near[u] ^ near[v = e[i].v])
        edt[++cnt] = edgeData(near[u], near[v], dis[u] + dis[v] + e[i].w);
    sort(edt + 1, edt + 1 + cnt);
}
int main() {
    n = read(), s = read(), m = read();
    rep(i, 1, n) fa[i] = i;
    rep(i, 1, s) C[i] = read();
    rep(i, 1, m) { int u = read(), v = read(), w = read(); add(u, v, w), add(v, u, w); }
    spfa();
    int q = read();
    rep(i, 1, q) qu[i].S = read(), qu[i].T = read(), qu[i].d = read(), qu[i].id = i;
    sort(qu + 1, qu + 1 + q);
    int pos = 1;
    rep(i, 1, q) {
        while (pos <= cnt && edt[pos].w <= qu[i].d) {
            int x = find(edt[pos].u), y = find(edt[pos].v);
            if (x ^ y) fa[x] = y;
            pos++;
        }
        ans[qu[i].id] = (find(qu[i].S) == find(qu[i].T));
    }
    rep(i, 1, q) puts(ans[i] ? "TAK" : "NIE");
    return 0;
}

转载于:https://www.cnblogs.com/aziint/p/8481500.html