2017-2018-1 20162316刘诚昊实验二树

最新推荐文章于 2025-08-12 21:03:53 发布

转载最新推荐文章于 2025-08-12 21:03:53 发布 · 113 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/ignor/p/7742006.html

文章标签：

#java #数据结构与算法

本文介绍了Java程序设计课程中的树结构实验，包括二叉树的实现、中序先序构造二叉树、决策树、表达式树、二叉查找树及红黑树分析等内容。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

20162316刘诚昊 2017-2018-2 《Java程序设计》第二次实验树

实验二树-1-实现二叉树：

实验要求：

参考教材p375,完成链树LinkedBinaryTree的实现（getRight,contains,toString,preorder,postorder）

用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试，提交测试代码运行截图，要全屏，包含自己的学号信息

课下把代码推送到代码托管平台

实验过程：

构建的树：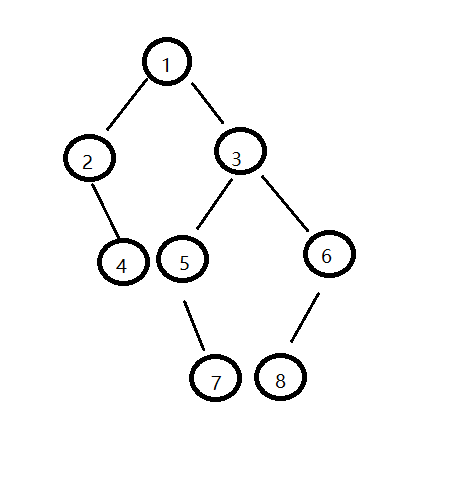

实验一中完成简单的步骤我就不在此加以赘述。

getRight:

public BinaryTree<T> getRight() {
        if (root == null)
            throw new EmptyCollectionException ("Get left operation "
                    + "failed. The tree is empty.");
        LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
        result.root = root.getRight();
        return result;
    }

contains:

 public boolean contains(T target) throws ElementNotFoundException {
        if (root == null)
            throw new ElementNotFoundException("Find operation failed. "
                    + "No such element in tree.");
        boolean a = false;
        BTNode<T> node = root.find(target);
        if (node != null ){
            a = true;
        }
        return a;

isEmpty:

 public boolean isEmpty() {
        return (root == null);
    }

preorder:

 public Iterator<T> preorder() {
        ArrayIterator<T> iter = new ArrayIterator<T>();
        if (root != null)
            root.preorder (iter);
        return iter;
    }

postorder:

 public Iterator<T> postorder() {
        ArrayIterator<T> iter = new ArrayIterator<T>();
        if (root != null)
            root.postorder (iter);
        return iter;
    }

我认为最难的地方在toString方法，一开始我调用levelorder方法,直接打印出后得到 [1,2,3,4,5,6,7,8]。后来问王老师后得知应当打印成就像书上这样：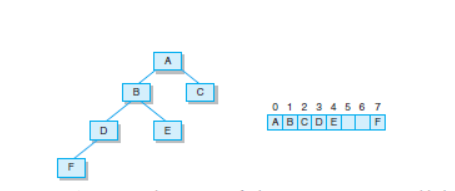

也即当遇到空的地方应当留一个位置出来而非略过。
于是我采用这样的方法：

 public String toString(){
        BTNode<T> To = root;  //将所要打印的树赋给一个新的节点，以避免后面的操作影响到原来的树
        int B = 0;
        String result = "";

        ArrayList<BTNode> list = new ArrayList(); 
        list.add(To); //将根加入到list队列中。

        //假如这个树为空，则直接返回一个空串；否则将根的元素转入String类型，加入到将要返回的结果中。
        if (To == null){
            return result;
            }
            else {
            result = To.getElement().toString();
        }

        //一个循环结构，每次循环遍历树的新一层节点，遍历list队列中的内容并在每次循环开始时创建一个新的数组L。
        //每次循环开始在打印结果中加入一个“ | ”,以区分不同层数，更易理解。
        while(B == 0){
            ArrayList<BTNode> L = new ArrayList();
            result = result + " |";
            String qaz = "";
        
        //当遍历遇到空节点，在数组L中加入两个空节点。
        //当遍历遇到非空节点，则将这个节点的左节点、右节点依次加入到数组L中，假若这个节点没有左（右）节点,便创建一个空的节点null，加入数组L中。
        //每次在打印空的节点时，用“口”代替。
        //把数组list的下一层节点的元素转化为String类型，再在下面判断是否加入打印的结果中。
            for(int c = 0; c<list.size();c++){
                if (list.get(c) == null){
                    qaz = qaz + " 口" + " 口";
                    L.add(null);
                    L.add(null);
                }
                else {
                    if (list.get(c).getLeft() == null) {
                        qaz = qaz + " 口";
                        L.add(null);
                    } else {
                        L.add(list.get(c).getLeft());
                        qaz = qaz + " " + list.get(c).getLeft().getElement();
                    }
                    if (list.get(c).getRight() == null) {
                        qaz = qaz + " 口";
                        L.add(null);
                    } else {
                        L.add(list.get(c).getRight());
                        qaz = qaz + " " + list.get(c).getRight().getElement();
                    }
                }
            }

            //遍历完一层以后得到下一层的节点，全部都在L中，此时把L赋给list，假若while循环未结束，则再次遍历list得到新的L。
            list =  L;

            //创建一个等于零的int类型，检查在最新的这个数组中，是否全部元素都是null。
            //假若不是，则把得到的新一层String类型加入到打印结果中，继续while循环。
            //假若是,则循环结束，得到结果result。
            int NUM = 0;
            for(int num = 0; num<list.size(); num++){

                if(list.get(num) == null)
                    NUM++;
                if (NUM==list.size())
                    B =1;
            }
            if (B==0)
                result = result + qaz;
        }
        return result;
}

以下是我的toString方法打印出的结果：

1 | 2 3 | 口 4 5 6 | 口 口 口 口 口 7 8 口 |

1-实现二叉树测试截图：

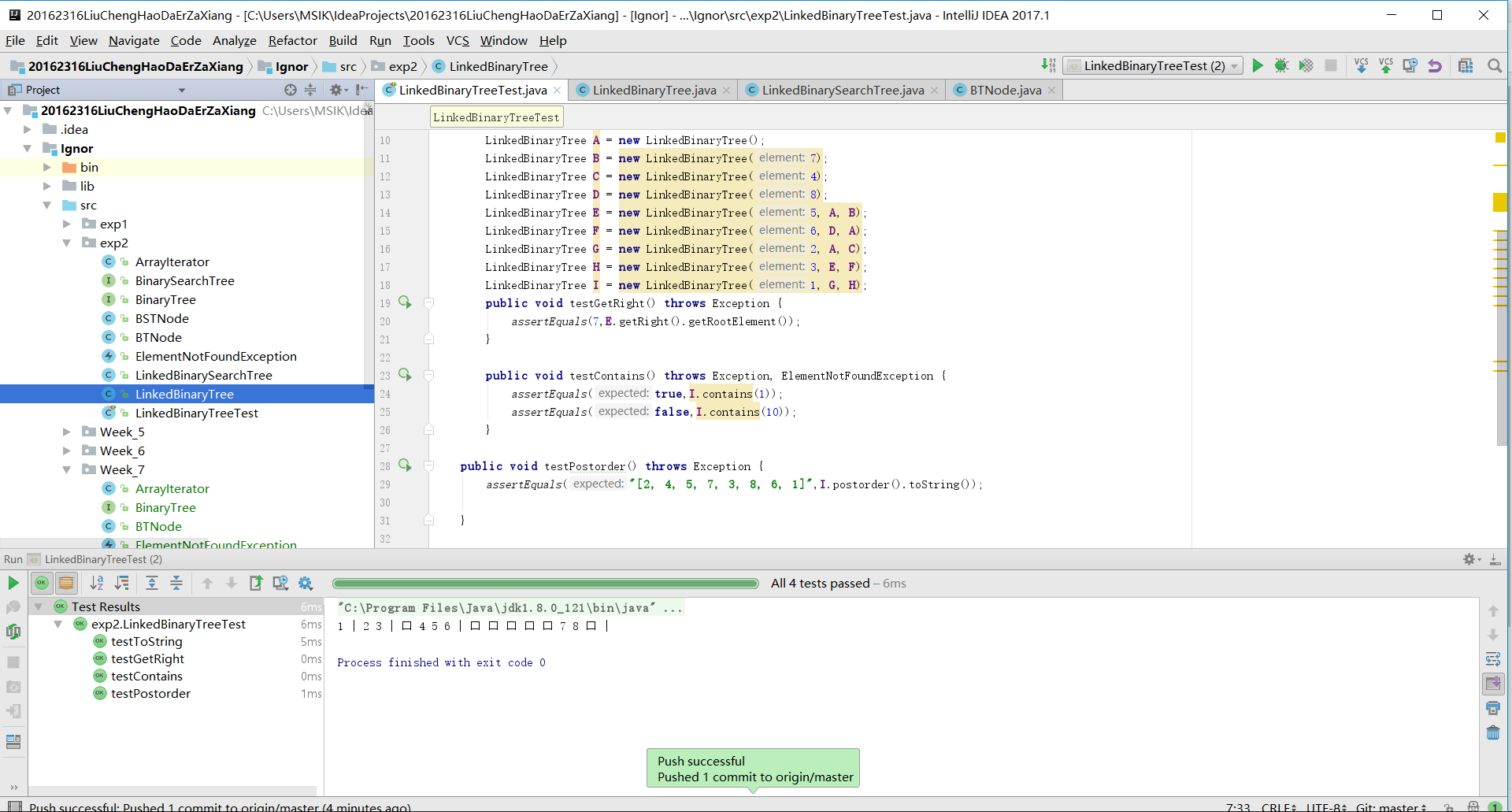
1-实现二叉树代码链接：

类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/LinkedBinaryTree.java

测试类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/LinkedBinaryTreeTest.java

实验二树-2-中序先序序列构造二叉树:

实验要求:

基于LinkedBinaryTree，实现基于（中序，先序）序列构造唯一一棵二㕚树的功能，比如教材P372，给出HDIBEMJNAFCKGL和ABDHIEJMNCFGKL,构造出附图中的树

用JUnit或自己编写驱动类对自己实现的功能进行测试，提交测试代码运行截图，要全屏，包含自己的学号信息

课下把代码推送到代码托管平台

实验过程：

这个实验我独自完成还有些力不足，于是参考了网上的代码：http://blog.youkuaiyun.com/leiflyy/article/details/51100687

在此我先引用先该代码的大方向思路：

例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}。

首先，根节点 是{ 1 }； 
左子树是：前序{ 2,4,7 } ，中序{ 4,7,2 }； 
右子树是：前序{ 3,5,6,8 } ，中序{ 5,3,8,6 }；

这时，如果我们把左子树和右子树分别作为新的二叉树，则可以求出其根节点，左子树和右子树。

这样，一直用这个方式，就可以实现重建二叉树。

再是我再码云中提交的实现功能的代码并加以阐释：

public class reConstructBinaryTree {
    //在此方法内输入先序、中序的数组。
    //如果两者任意数组为空，返回为空。
    //例如我现在输入的先序数组为{1,2,4,7,3,5,6,8}，中序为{4,7,2,1,5,3,8,6}。
    public  BTNode reConstructBinaryTr(int [] pre, int [] in) {
        if(pre == null || in == null){
            return null;
        }
        BTNode qw = reCons(pre, in, 0, pre.length-1, 0, in.length-1);
        return qw;
    }

    //主函数，用来构建树。
    public  BTNode reCons(int[] pre, int[] in, int preStart, int preEnd, int inStart, int inEnd) {
        //建立一个节点，使用先序排列的第零个作为其元素。
        BTNode tree = new BTNode(pre[preStart]);
        tree.left = null;
        tree.right = null;
        //假若此时先序排列和中序排列中元素仅有一个，便就此返回，上面创立的节点便为叶。
        if (preStart == preEnd && inStart == inEnd) {
            return tree;
        }
        //这里的root用来计算子树的节点数。
        //比如：
        //以上我输入的先序数组的第零个为“1”，与中序的第四个元素相同，那么此时root为3.
        //也即，接下来的左子树有3个节点，右子树则有4个节点（中序遍历的数组中，“1”后面有4个元素。
        int root = 0;
        for(root= inStart; root < inEnd; root++){
            if (pre[preStart] == in[root]) {
                break;
            }
        }
        int leifLength = root - inStart;
        int rightLength = inEnd - root;
        //如果左子树的节点数大于0，开始递归构建左子树。右子树同样如此。
        if (leifLength > 0) {
            tree.left = reCons(pre, in, preStart+1, preStart+leifLength, inStart, root-1);
        }
        if (rightLength > 0) {
            tree.right = reCons(pre, in, preStart+1+leifLength, preEnd, root+1, inEnd);
        }
        return tree;
    }

2-中序先序序列构造二叉树测试：

测试中仍然使用这棵树：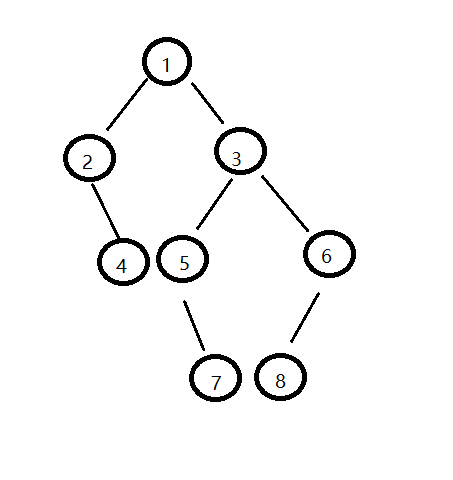

调用类中再中序遍历的操作，看是否与输入一致：
中序遍历代码：

public void preTraverseBinTree(BTNode node){
        ArrayIterator iter = new ArrayIterator();
        if (node != null)
            node.preorder (iter);
        System.out.println(iter);
    }

测试截图：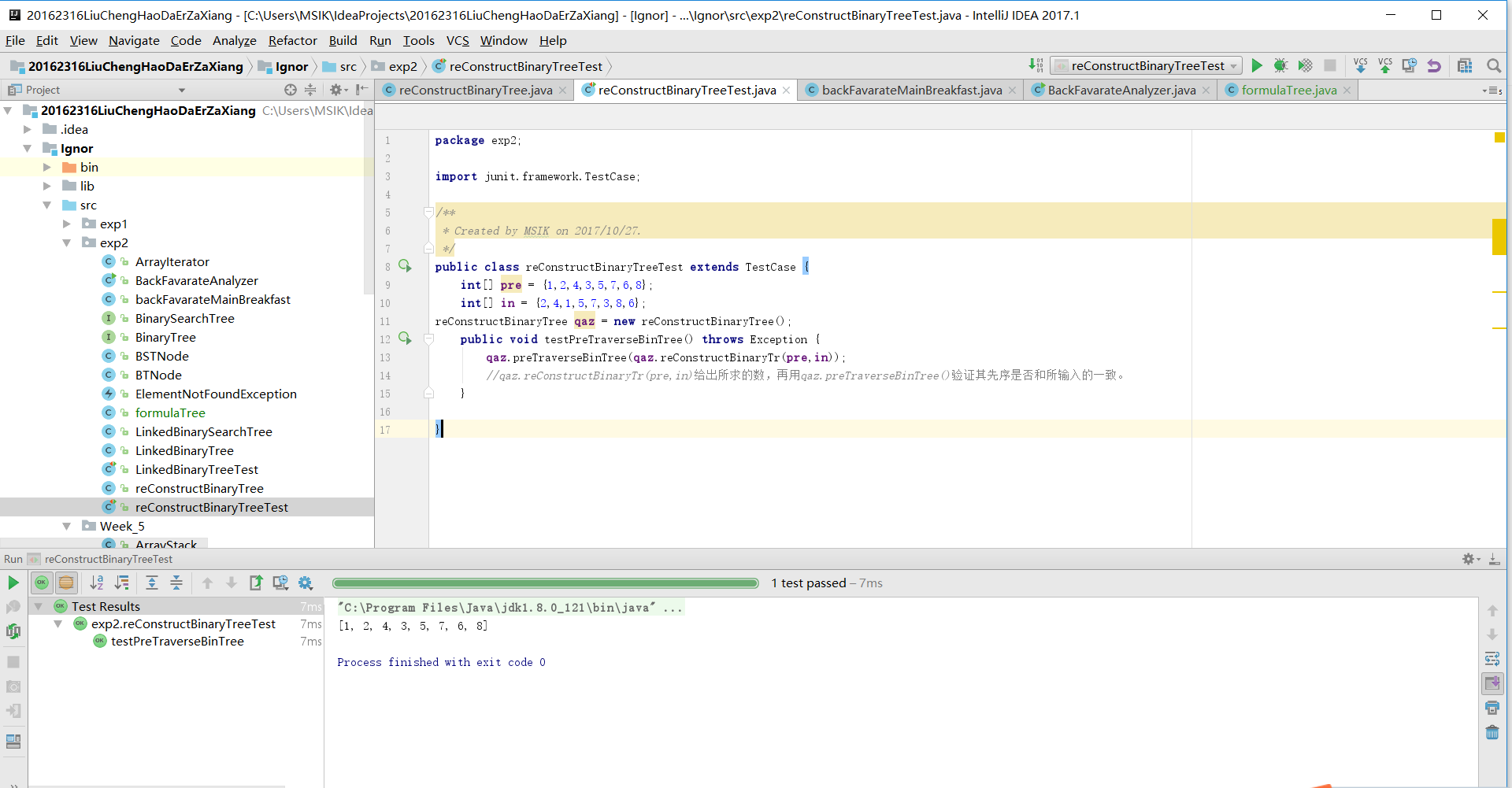

2-中序先序序列构造二叉树代码链接：

实现类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/reConstructBinaryTree.java

测试类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/reConstructBinaryTreeTest.java

实验二树-3-决策树：

实验要求：

完成PP16.6：在称为20问的游戏中，一个人先想好一个物体，另一个人通过 yes-or-no 问题尝试判定这个物体是什么。目标是用尽可能少的问题判定出物体。设计并实现程序，利用决策树来玩20问游戏，基于一组预设的可能的物体。

提交测试代码运行截图，要全屏，包含自己的学号信息

课下把代码推送到代码托管平台

实验过程：

我设计的问题是关于猜测最喜欢的早餐主食：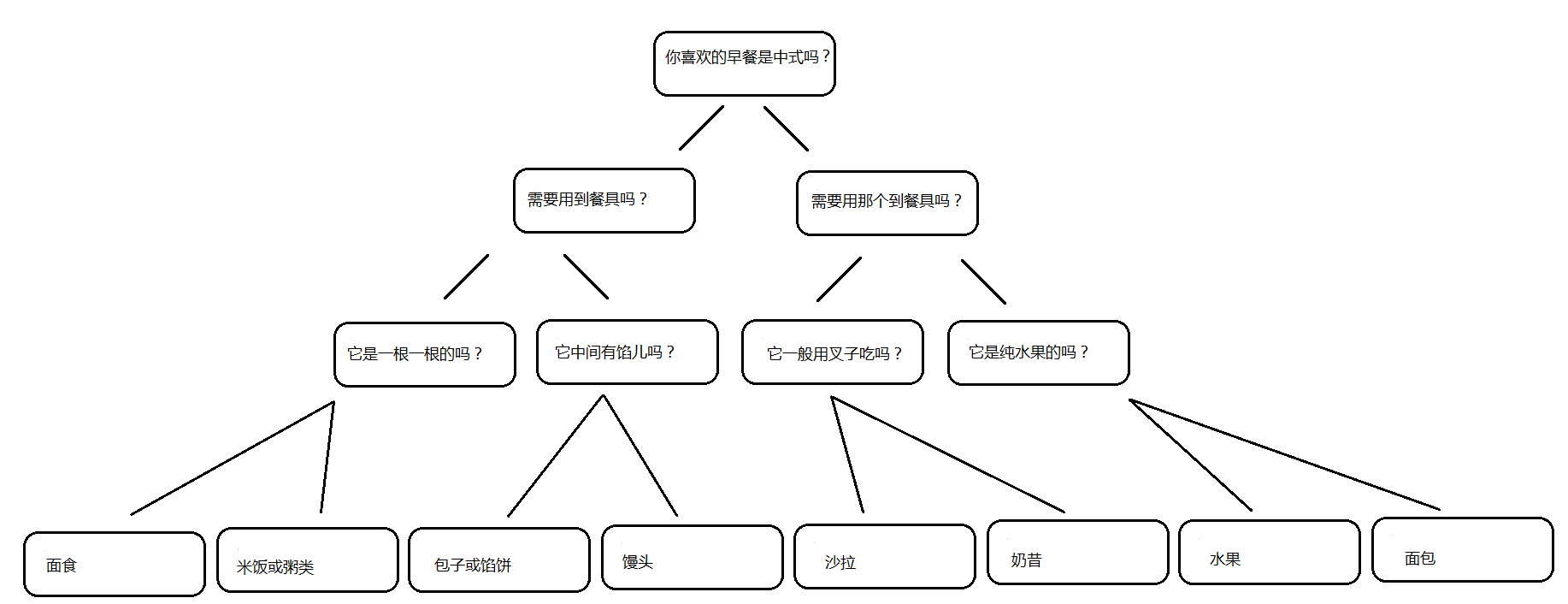

这个实验很简单跟着书上走就行了。

树-3-决策树测试截图：

树-3-决策树代码链接：

实现类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/backFavarateMainBreakfast.java

决策：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/BackFavarateAnalyzer.java

实验二树-4-表达式树：

实验要求：

完成PP16.8：第二章介绍过，表达式树可用来表示算术表达式。设计并实现程序，使用二叉树来表示表达式树。提供方法对数进行计算，得到表达式的结果。

提交测试代码运行截图，要全屏，包含自己的学号信息

课下把代码推送到代码托管平台

实验过程：

构建一棵表达式树：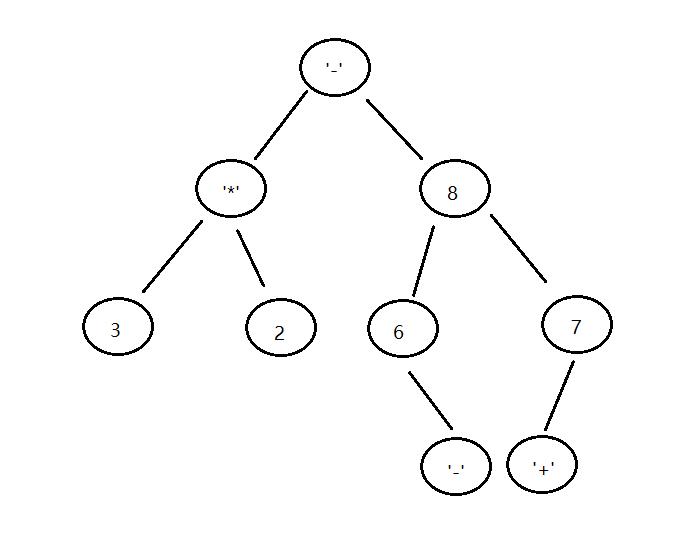

构建以后用中序遍历得出中缀表达式，再用上个学期四则运算的代码转化为后缀并得出结果：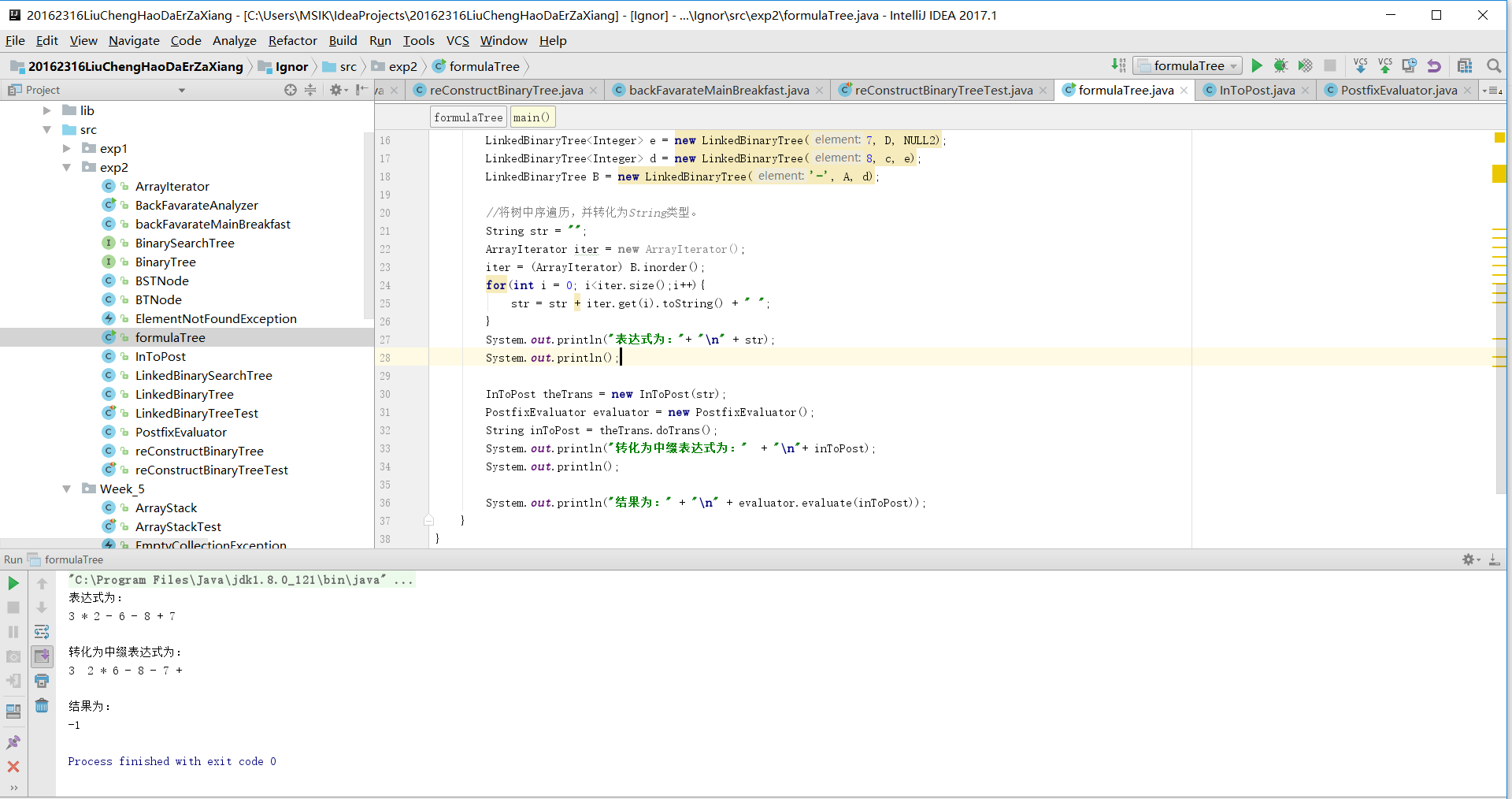

4-表达式树代码链接：

https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/formulaTree.java

实验二树-5-二叉查找树：

实验要求：

完成PP17.1：完成本章中LinkedBinarySearchTree类的实现。特别是实现findMin和findMax两个操作。

提交测试代码运行截图，要全屏，包含自己的学号信息

课下把代码推送到代码托管平台

实验过程：

findMin：
先创一个节点node赋值为root；
当root为null，直接返回为null；
当root不为null时，进入while循环结构；
只要当前节点有左枝，便该左枝取代原node称为新的node；
直到没有左节点时，返回node的元素。

 public T findMin() {
        if(root == null){
            return null;
        }
        BSTNode<T> miner  = (BSTNode<T>) root;
        while(miner.getLeft() != null) {
            miner = (BSTNode<T>) miner.getLeft();
        }
        return miner.getElement();
    }

findMax类似。

实验二树-5-二叉查找树测试：

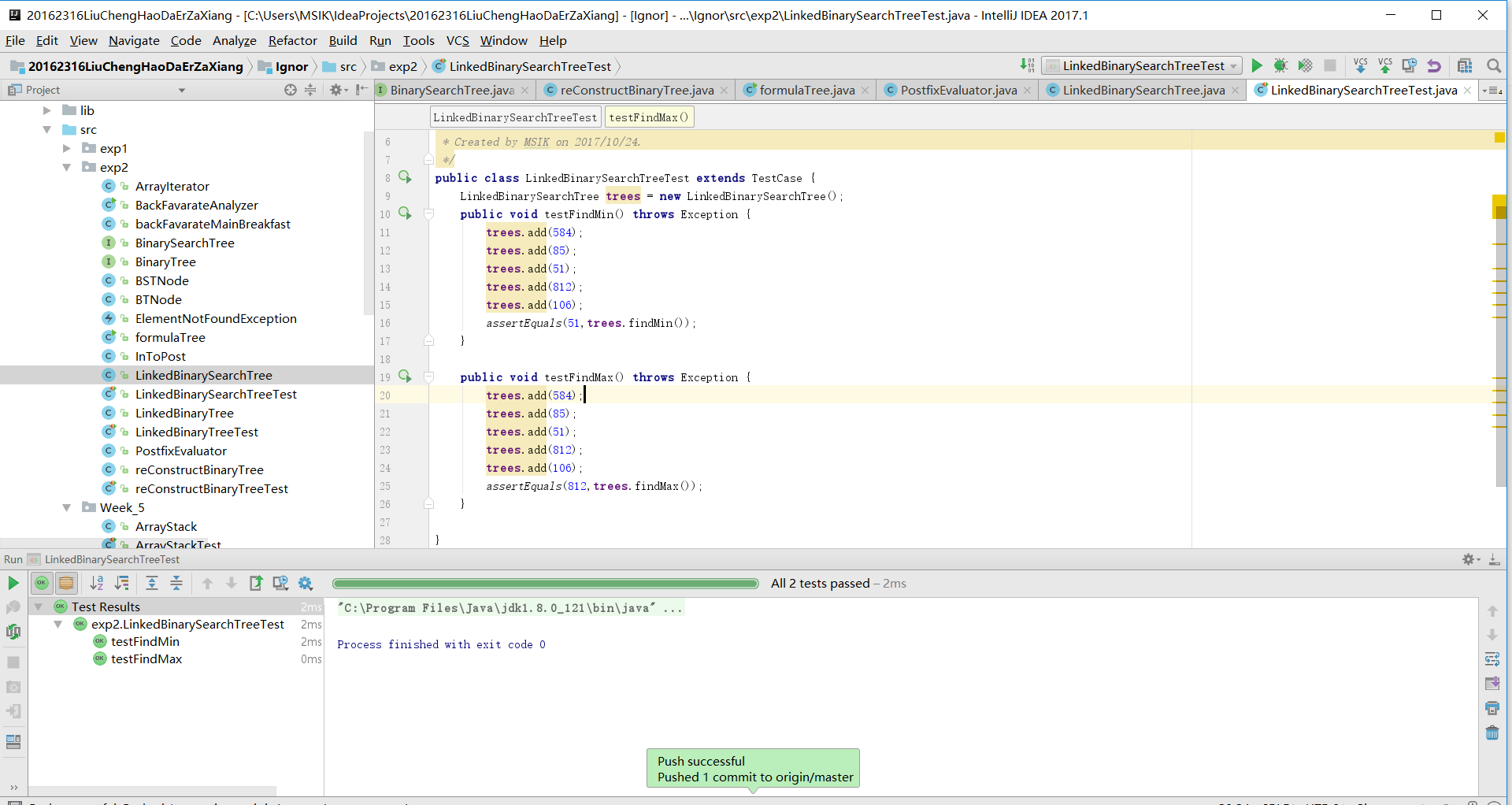
实验二树-5-二叉查找树代码链接：

实现类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/LinkedBinarySearchTree.java

测试类：https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp2/LinkedBinarySearchTreeTest.java

实验二树-6-红黑树分析：

实验要求：

参考 http://www.cnblogs.com/rocedu/p/7483915.html 对Java中的红黑树（TreeMap，HashMap）进行源码分析，并在实验报告中体现分析结果.

实验过程：

首先要了解红黑树是什么，这里引用360百科中有关红黑树的部分：

红黑树(Red Black Tree) 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。
它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的"红黑树"。
红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。
它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的: 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

它在除了二叉查找树的性质外，还有：

性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点(NIL节点，空节点)是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

在红黑树上只读操作不需要对用于二叉查找树的操作做出修改，因为它也是二叉查找树。但是，在插入和删除之后，红黑属性可能变得违规。恢复红黑属性需要少量(O(log n))的颜色变更(这在实践中是非常快速的)并且不超过三次树旋转(对于插入是两次)。这允许插入和删除保持为 O(log n) 次，但是它导致了非常复杂的操作。

如果插入根节点，那么性质2便会被破坏，这时便需要进行旋转：

左旋：

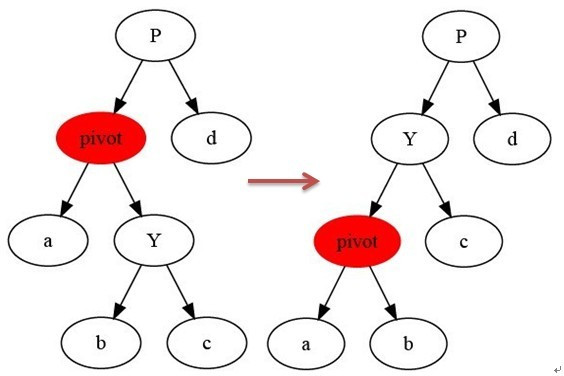
private void leftRotate(RBTNode<t> x) {
    // 设置x的右孩子为y
    RBTNode<t> y = x.right;
 
    // 将 “y的左孩子” 设为 “x的右孩子”；
    // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”
    x.right = y.left;
    if (y.left != null)
        y.left.parent = x;
 
    // 将 “x的父亲” 设为 “y的父亲”
    y.parent = x.parent;
 
    if (x.parent == null) {
        this.mRoot = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
    } else {
        if (x.parent.left == x)
            x.parent.left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        else
            x.parent.right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
    }
     
    // 将 “x” 设为 “y的左孩子”
    y.left = x;
    // 将 “x的父节点” 设为 “y”
    x.parent = y;
}

右旋：

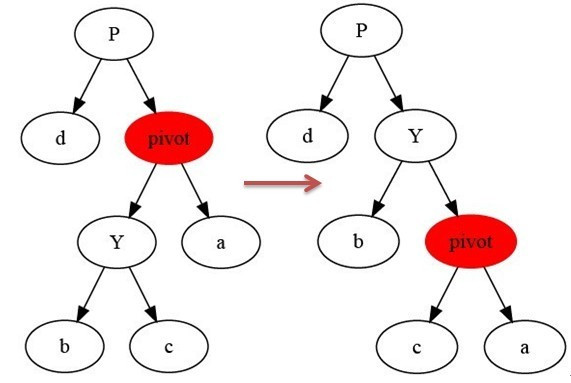
private void rightRotate(RBTNode<t> y) {
    // 设置x是当前节点的左孩子。
    RBTNode<t> x = y.left;
 
    // 将 “x的右孩子” 设为 “y的左孩子”；
    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
    y.left = x.right;
    if (x.right != null)
        x.right.parent = y;
 
    // 将 “y的父亲” 设为 “x的父亲”
    x.parent = y.parent;
 
    if (y.parent == null) {
        this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
    } else {
        if (y == y.parent.right)
            y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }
 
    // 将 “y” 设为 “x的右孩子”
    x.right = y;
 
    // 将 “y的父节点” 设为 “x”
    y.parent = x;
}