PSPACE是计算复杂度理论中能被确定型图灵机利用多项式空间解决的判定问题集合。
形式化定义
如果规定  为至多
为至多 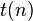 空间内能被确定型图灵机解决的问题的集合(
空间内能被确定型图灵机解决的问题的集合( 是输入大小
是输入大小  的函数),那么,PSPACE可被形式化地定义为:
的函数),那么,PSPACE可被形式化地定义为:
PSPACE真包含上下文有关语言,这种语言等价于线性有界非确定图灵机。
尽管至今没有证明,但一般认为,将P中的确定型图灵机更改为非确定图灵机后得到的NP类有 成立。然而,对于PSPACE,将确定型图灵机更改为非确定型图灵机,得到的NPSPACE并不比PSPACE大。原因是根据萨维奇定理,
成立。然而,对于PSPACE,将确定型图灵机更改为非确定型图灵机,得到的NPSPACE并不比PSPACE大。原因是根据萨维奇定理,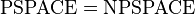 ,这个定理的结论指出,虽然非确定性问题需要更多时间解决,两者的空间需求还是一致的。
,这个定理的结论指出,虽然非确定性问题需要更多时间解决,两者的空间需求还是一致的。
PSPACE完全
如果所有PSPACE中的问题都可以多项式时间归约到某个问题,那么,这个问题可以被定义为PSPACE难。
一种语言B为PSPACE完全,如果它在PSPACE中,并且为PSPACE难,即
其中, 指的是存在从A到B的多项式时间归约。PSPACE完全问题对于研究PSPACE中的问题非常重要,因为它们代表了PSPACE中最困难的问题。如果一个PSPACE完全问题得到了时间上高效的算法,那么,对所有PSPACE中的问题都可以有时间上高效的算法,因为这些问题都能够被多项式时间归约到PSPACE完全问题。然而,这个性质对PSPACE难不成立,因为存在这样的问题,它们可能属于PSPACE难但不属于PSPACE完全,因为这些问题不属于PSPACE。
指的是存在从A到B的多项式时间归约。PSPACE完全问题对于研究PSPACE中的问题非常重要,因为它们代表了PSPACE中最困难的问题。如果一个PSPACE完全问题得到了时间上高效的算法,那么,对所有PSPACE中的问题都可以有时间上高效的算法,因为这些问题都能够被多项式时间归约到PSPACE完全问题。然而,这个性质对PSPACE难不成立,因为存在这样的问题,它们可能属于PSPACE难但不属于PSPACE完全,因为这些问题不属于PSPACE。
围棋的复杂度已于1978年被Robertson与Munro证明为PSPACE-hard




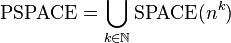

















 8457
8457

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








