Trie 简介

最新推荐文章于 2025-03-19 15:10:25 发布

转载最新推荐文章于 2025-03-19 15:10:25 发布 · 157 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/xiaoyh/p/10407815.html

本文深入探讨Trie树（字典树）的概念，解析其如何利用字符串的公共前缀提高查询效率，避免不必要的字符遍历，从而实现高效检索。文章提供了一个简单的Trie树Java代码实现，包括插入、深度遍历和搜索功能。

一、Trie简介

　　在计算机科学中，Trie，又称字典树、前缀树、单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

　　Trie树主要是利用词的公共前缀缩小查词范围、通过状态间的映射关系避免了字符的遍历，从而达到高效检索的目的。

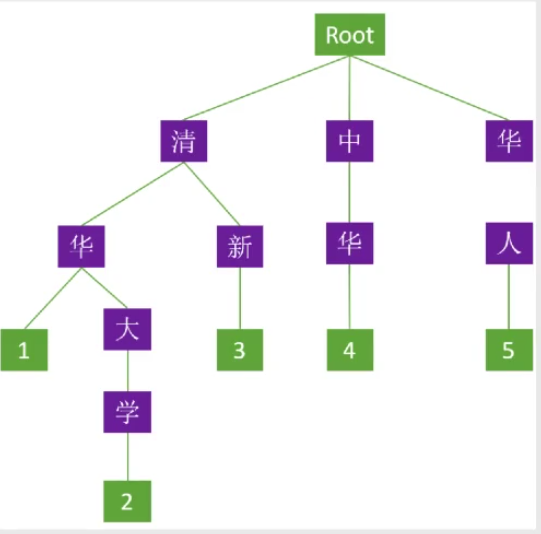
二、简单代码实现

　　1、结点类

 1 public class TrieNode {
 2     int level;
 3     // 只针对英文小写字母
 4     TrieNode[] children = new TrieNode[26]; // 子节点信息
 5     TrieNode parent; // 当前节点的父节点
 6 
 7     public boolean isLast;
 8 
 9     public int fre = 1;// 出现频率
10 }

View Code

　　2、Trie类

 1 public class Trie {
 2     TrieNode root;
 3 
 4     public Trie() {
 5         root = new TrieNode();
 6     }
 7 
 8     public void insert(String str) {
 9         char[] chars = str.toCharArray();
10         TrieNode p = root;
11         // 遍历单词的每个字符
12         for (int i = 0; i < chars.length; i++) {
13             char c = chars[i];
14             TrieNode child = p.children[c - 'a'];
15             if (child == null) {
16                 TrieNode nnode = new TrieNode();
17                 nnode.level = i;
18                 p.children[c - 'a'] = nnode;
19                 p = nnode;
20             } else {
21                 p = child;
22                 child.fre++;
23             }
24         }
25         p.isLast = true;
26     }
27 
28     /**
29      * 深度遍历
30      */
31     public void printAll() {
32         print("", root);
33     }
34 
35     private void print(String prefix, TrieNode p) {
36         if (p.isLast && prefix.length() > 0) {
37             System.out.println(prefix + " " + p.fre);
38         }
39         for (int i = 0; i < 26; i++) {
40             if (p.children[i] != null) {
41                 print(prefix + (char) ('a' + i), p.children[i]);
42             }
43         }
44     }
45 
46     public void search(String prefix) {
47         char[] chars = prefix.toCharArray();
48         TrieNode p = root;
49         for (int i = 0; i < chars.length; i++) {
50             char c = chars[i];
51             TrieNode child = p.children[c - 'a'];
52             if (child == null) {// 结算
53                 return;
54             } else {
55                 p = child;
56             }
57         }
58         print("", p);
59     }
60 
61 }