day_3:z分数、正态分布和概率

最新推荐文章于 2025-08-08 00:32:30 发布

weixin_30882895

最新推荐文章于 2025-08-08 00:32:30 发布

阅读量1.7k

点赞数

CC 4.0 BY-SA版权

文章标签： java

原文链接：http://www.cnblogs.com/jp-mao/p/9797348.html

本文详细介绍了Z分数的概念，包括其组成、计算公式及在正态分布中的应用。Z分数能够显示原始分数与均值之间的标准差数量，用于标准化分布，便于不同分布间的分数比较。同时，文章还解释了Z分数在判断分数位置、代表概率和变量关系中的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

z分数

　　又正负符号和数值两个部分组成，正号表示分数比均值大，负号表示比均值小，数值表示的是原始分数和均值之间差几个标准差

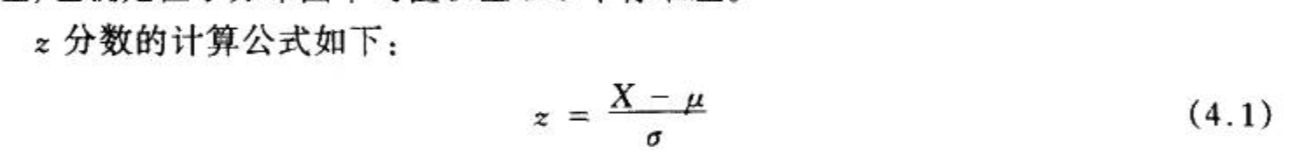
注：z=（原始分数-算术平均数）/标准差

z分数和标准分布

z分数的另一用途是把整个分布标准化

z分数分布的特征：

z分数分布的形状和未转换前的原始分布的形状完全相同

z分数分布的均值一定为0

z分数分布的标准差一定为1

z分数的意义

判断分数在分布中的位置信息，使整个分布标准化，易于在两个分布中进行分数比较

z分数可以代表概率

z分数代表变量间的关系

正态分布

概率：从总体中得到特定的样本的可能性

　　特定样本的概率=特定样本出现的次数/可能出现的结果的总数

转载于:https://www.cnblogs.com/jp-mao/p/9797348.html

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

weixin_30882895

关注关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

Day 2: Scikit-learn深入与经典算法详解

weixin_44903776的博客

07-21

1. 理解线性回归和逻辑回归的工作原理 2. 掌握决策树的分割逻辑 3. 了解随机森林的集成思想 4. 学会使用Scikit-learn的标准流程 5. 完成两个经典项目：鸢尾花分类和房价预测

Day 10: Mini-GPT完整手写实战 - 从组件组装到文本生成的端到端实现

最新发布

weixin_44903776的博客

08-12

本文介绍了Mini-GPT的完整实现过程，包括数据预处理、模型架构和训练流程。文章首先对比了GPT和BERT的架构差异，强调GPT作为生成式模型的特性。然后详细展示了字符级分词器的构建、文本数据集的准备，以及核心组件MultiHeadAttention的实现。整个实现采用PyTorch框架，重点关注了因果注意力掩码、残差连接等关键设计，为理解GPT类语言模型的工作原理提供了实践基础。

参与评论您还未登录，请先登录后发表或查看评论

概率论：样本与总体分布，Z分数与概率

weixin_47198715的博客

05-25

3974

如何理解样本和整体的关系，利用Z分位数来品评估样本是否能够代表总体，这是假设检验的基础，当年就是没有完整理解这一点，导致概率论学的一知半解的

z分数查找：从z分数到概率。

02-16

Z分数查询从z得分到概率...

正态分布概率表

11-20

希望可以帮到大家，直接是概率度t对应函数F(t),方便查看

【统计至简】z分数是什么

qq_39400324的博客

03-09

859

z 分数表示的是某个数据值与数据集均值之间的距离，这个距离是以标准差为单位来衡量的。计算公式：对于一个给定的数据集x1x2xnx1x2...xn，其均值为μ\muμ，标准差为σ\sigmaσ，那么数据集中某一具体数据xxx的zzz分数zzz的计算公式为zx−μσzσx−μ。例如，某个班级学生的考试成绩均值为 80 分，标准差为 10 分，小明的成绩是 90 分，那么小明成绩的 z 分数为z90−80101。

标准正态分布面积（面积=比例=概率，不仅限于正态分布）

zhanghongxian123的专栏

09-02

9万+

对于一组数据，服从（均值0,1）

【Day1-AM_CONVERGE数据管理秘籍】：高效处理与分析数据的3大策略

[【Day1-AM_CONVERGE数据管理秘籍】：高效处理与分析数据的3大策略](https://p1-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/31f1da845c1e4b3f982b2371cbc4d9c2~tplv-k3u1fbpfcp-zoom-in-crop-mark:1512:0:0:0.awebp?...

Day 7: RNN循环神经网络 - 序列数据的记忆大师

weixin_44903776的博客

08-08

摘要： RNN（循环神经网络）是专为序列数据设计的神经网络，通过隐藏状态传递历史信息，使其具备处理时间序列、文本等能力。核心机制为循环结构，每个时间步的输出依赖当前输入和之前状态（公式：h_t = tanh(W_hh * h_{t-1} + W_ih * x_t + b_h)）。PyTorch实现展示了RNN的逐步处理过程。但其存在梯度消失/爆炸、长期依赖和并行性差等局限，可通过LSTM/GRU、梯度裁剪和注意力机制优化。RNN是机器翻译、语音识别等任务的基础模型。关键词： RNN、序列数据、隐藏状态、梯

逆正态变换python

02-26

此过程涉及将原始数据转换为累积分布函数(CDF)，再通过标准正态分布的分位数函数将其映射到正态分布。对于列级别的操作[^1]，可以应用这些统计变换而无需影响整个DataFrame结构： ```python import numpy as np ...

标准正太分布查表求概率

05-21

标准正太分布积分查表求概率，一般高斯过程标准化后也就可以查找此表了

知识体系_统计学_21_概率分布表

geilip的博客

03-16

1325

在利用样本统计量对总体参数进行区间估计和假设检验时，样本统计量的常见的概率分布主要有：正态分布、t分布、分布、F分布等，本文将提供这几种概率分布的概率表，便于需要查找概率值时使用。

正态分布概率表_三、统计概率思维

weixin_39899021的博客

12-09

6514

一、误差思维（只要有估计，就会有误差）1.误差永远存在，并且不可避免。2.多次测量用平均值的统计方式取得结果，尽量避免偶然因素的影响。二、置信区间（误差范围）1.统计学最核心思想：用样本信息估计总体信息。2.点估计：这个总体中的一个样本平均值就是对总体平均值的一次点估计。3.置信水平：表示置信区间包含总体平均值的概率是多大。4.置信区间：由样本统计量所构造的总体参数的估计区间。三、小样本和大样本的...

概率论 - 常见分布（及其分布表）

壮壮不太胖的学习笔记

04-19

5万+

离散型的分布一，0-1分布有2种结果，实验只做1次。 P(X = k) = pk(1-p)1-k 数学期望：E(X) = p 方差：Var(X)=p(1-p) 二，几何分布 P(A) = p，事件A在第k次首次发生（前k-1次均未发生）。记作：X ~ G(p) P(X = k) = (1-p)k-1p 数学期望：1/p 方差：(1-p)/p2 三，二项分布 P(A) = p，在n次...

正态分布某一点的概率怎么算_标准正态分布+标准正态分布概率表+分布函数+积分...

weixin_39841640的博客

01-17

7486

X~N(μ,σ²)：一般正态分布：均值为μ、方差为σ²http://blog.youkuaiyun.com/zhanghongxian123/article/details/39008493对于标准正态分布来说，存在一张表，称为：标准正态分布表：该表计算的是：P(X<=x)【某个数落在某个[-@,x]】的概率。也就是下面阴影图形所示的面积：如果x=1.96.则将1.96拆分为1.9和0.06.横轴1.9...

Excel图表—标准正态分布概率分布图（概率密度函数图及累积概率分布图）的绘制

预见未来to50的专栏

10-12

5万+

看似很简单的一张Excel图表，实际上也花了10多分钟。这对于已经习惯了Spotfire这种数据可视化软件的我而言是不能接受的。不过，功夫不负有心人，总算是画出了教科书上的效果。以下是一点小创新，如果提高数据粒度（数据粒度能够满足业务要求），有些问题的答案将一目了然。比如，问题：假定某种股票的收益率呈标准正态分布，确定0.5的随机变量值对应的标准正态分布函数值（累积...

正态分布及其概率计算