schwarz（ 施瓦兹）不等式证明

证明

如果： 函数 y=ax^2+2bx+c 对任意x >=0 时 y>=0;

函数图象在全部x轴上方，故二次方程判别式 b^2-4ac<=0;(即方程无实数解)

即(2b)^2<=4ac  =>  b^2<ac;

 

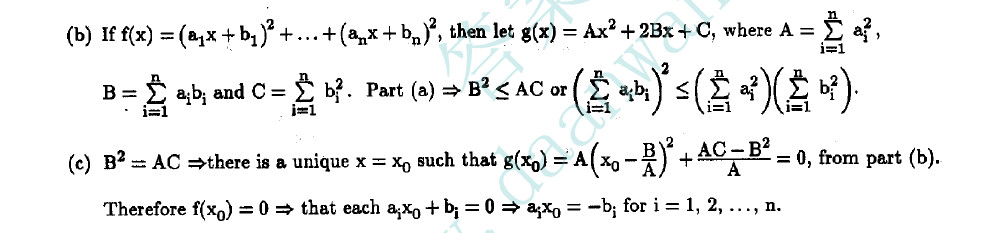
注意:上面g(x0)A(x0-B/1)^2 中X0-B/A 应该表示成(X0+B/A);参考判别式:

http://baike.baidu.com/link?url=pwwiWoBpl4yNww_tA7mbm3tcZsIYGuw40GScqkgYiUUsykFWFXsWvLzGsgFtE7nrnqCkox0cgzUhM3rCK8cjTq

注意教程上(P338 schwarz表达式证明中) ax^2+bx+c 应该写成ax^2+2bx+c 

 

转载于:https://www.cnblogs.com/wdfrog/p/5680148.html