from https://www.zhihu.com/question/30672734
下面从梯度与方向导数的关系来解释:
1 方向导数
-
引入
原来我们学到的偏导数指的是多元函数沿坐标轴的变化率,但是我们往往很多时候要考虑多元函数沿任意方向的变化率,那么就引出了方向导数
-
定义
(1)方向导数是个数值。
二维空间情形:
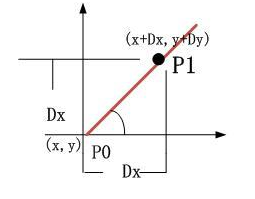
我们把f(x+Dx,y+Dy)-f(x,y)的值Value1与PP1的距离value2的比值的极值叫做沿PP1的方向导数。
三维空间计算过程相似;
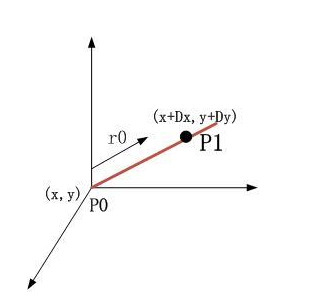
换句话来说,方向导数就是研究在某一点处的任意方向的变化率~
2 梯度
首先我来说,梯度是一个向量,并不是原来方向导数说的那样是一个数,那么这个向量是什么特殊的向量呢?还需要拿出来单独研究,那就是梯度代表的是各个导数中,变化趋势最大的那个方向,下面来介绍~
-
定义
-

 证明
证明
梯度方向就是方向导数最大的方向,我们看如下:

只有当Θ为0度的时候(
 ),方向导数最大(左边的式子),也就是说方向导数什么情况下最大,就是它的方向(
),方向导数最大(左边的式子),也就是说方向导数什么情况下最大,就是它的方向( ,
, )(这个方向公式中表示用x,y轴的线性组合表示了)和梯度方向一样(
)(这个方向公式中表示用x,y轴的线性组合表示了)和梯度方向一样( )(平行)的时候,这个方向导数是最大的....换句话也可以说,方向导数任意方向一定有个变化率最大的方向,这个时候,我们把这个最大的方向定义为梯度方向~
)(平行)的时候,这个方向导数是最大的....换句话也可以说,方向导数任意方向一定有个变化率最大的方向,这个时候,我们把这个最大的方向定义为梯度方向~
作者:忆臻
链接:https://www.zhihu.com/question/30672734/answer/139402480
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。




















 1399
1399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








