数学基础 莫比乌斯反演

Chapter 9. 数学基础 莫比乌斯反演

写在前面：首先感谢PoPoQQQ的ppt，感谢outer_form的证明.

然后我想说一定是我太智障了！

 

进入正题：

莫比乌斯反演公式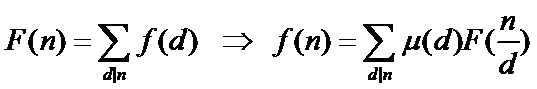：，关于证明我们在后面说.

其中的μ(d)是莫比乌斯函数，定义如下：

①当d=1，μ(d)=1

②当d=p₁*p₂*p_3^…p_k，p_i为互异素数，那么μ(d)=（-1）^k

③当d为其他时，μ(d)=0

那么对于任意正整数n有：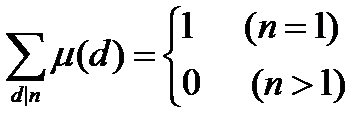

证明：

①当n=1时，值为1

②当n≠1时，将n分解为p₁^a₁p₂^a₂…p_k^a_k，p1,p2…pk为n的质因子，在n的所有因子中，μ值不为0的只有 所有质因子次数都是1 的因子，在这些因子中 质因子的个数为r  的因子有C^r_k个，那么我们可以得到

 

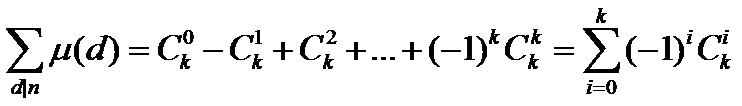
 此时我们要证明，根据二项式定理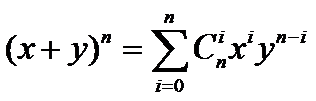，令x=-1,y=1,代入即可得证.

 

 

然后我们来证明莫比乌斯反演的公式

 

对于公式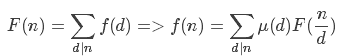

 

恒等变形得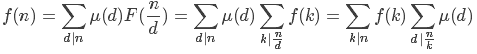,因为d|n  k|n/d，所以d*x=n   k*y=n/d，所以k*y*d=n，所以k|n,d|n/k

此前我们证明了

 

所以当且仅当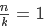，即n=k时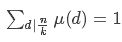，，其他情况都等于0.

所以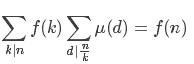，得证.

 

莫比乌斯反演定理还有第二种形式

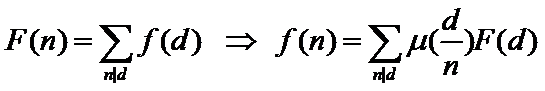
证明：

  

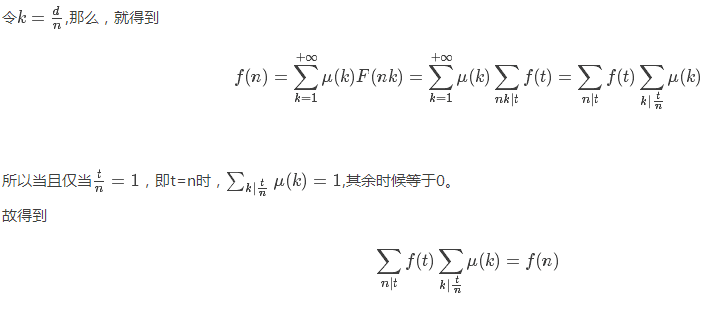
得证.

以上两个证明来自outer_form

 

 

关于莫比乌斯函数的性质

①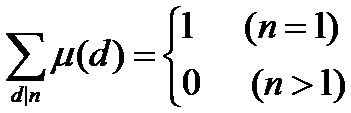

 

②

③莫比乌斯函数是一个完全积性函数，积性函数具有：f(1)=1和积性函数的前缀和也是积性函数的性质.

 

 

代码：

//利用欧拉筛法来求解莫比乌斯函数
int Euler(int n){
    memset(Mob,0,sizeof(Mob));
    Mob[1]=1;
    memset(flag,false,sizeof(flag));
    
    for (int i = 2; i <= n; i++)
    {
        if (!flag[i]) {
           prime[++cntprime] = i;
           Mob[i]=-1;
        }
        for (int j = 1; j <= cntprime && prime[j]*i <= n; j++)          {
             flag[i*prime[j]] = true;
             if (i % prime[j] == 0) {
               Mob[prime[j]*i]=0;
               break;
             }
             else Mob[prime[j]*i]=-Mob[i];
         }
    }
    return cntprime;
}

 

应用：对于一些函数f(n)，如果我们很难直接求出它的值，而容易求出倍数（第二种形式）和或约数（第一种形式）和F(n)，那么我们可以通过莫比乌斯反演来求得f(n)的值

 

 

 

再次感谢PoPoQQQ的ppt，感谢outer_form的证明.

 

 

---

肖申克的救赎

 

我希望跨越边境，

与朋友相见握手。

我希望，

太平洋的海水如同梦中一样的蓝。

我希望，

人生可以归结为一种简单的选择：

汲汲而生，汲汲而死。

 

 

---

 

 Sylvia

二零一七年七月二十日

 

转载于:https://www.cnblogs.com/jasmine-lee/p/7210133.html