bzoj2301[HAOI2011]Problem b

最新推荐文章于 2019-05-19 11:42:23 发布

转载最新推荐文章于 2019-05-19 11:42:23 发布 · 57 阅读

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/lcxer/p/10242897.html

本文探讨了一种在二维平面上进行查询优化的方法，通过固定左端点将问题转化为平面内的矩形区域查询，利用差分技巧减少重复计算。文中详细介绍了solve函数的实现，该函数用于计算特定范围内满足条件的数对数量，并通过实例代码展示了如何运用预处理和快速求解策略提高效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

传送门

这个题比起[POI2007]ZAP-Queries固定了左端点，我们可以把它画成一个二维的平面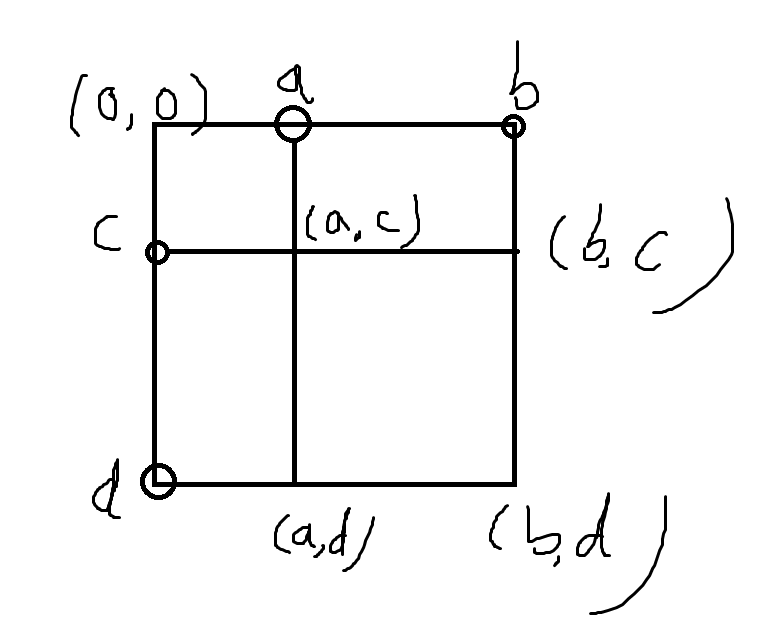

那么\[ans=solve((1,b),(1,d))-solve((1,b),(1,c-1))-solve((1,a-1),(1,d))+solve((1,a-1),(1,c-1))\]
solve部分的推导可以参考[POI2007]ZAP-Queries
代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
void read(int &x) {
    char ch; bool ok;
    for(ok=0,ch=getchar(); !isdigit(ch); ch=getchar()) if(ch=='-') ok=1;
    for(x=0; isdigit(ch); x=x*10+ch-'0',ch=getchar()); if(ok) x=-x;
}
#define rg register
const int maxn=5e4;
int n,a,b,c,d,k,mu[maxn+1],tot,pri[maxn+1];bool vis[maxn+1];
void prepare()
{
    mu[1]=1;
    for(rg int i=2;i<=maxn;i++)
    {
        if(!vis[i])pri[++tot]=i,mu[i]=-1;
        for(rg int j=1;j<=tot&&pri[j]*i<=maxn;j++)
        {
            vis[pri[j]*i]=1;
            if(i%pri[j])mu[pri[j]*i]=-mu[i];
            else {mu[pri[j]*i]=0;break;}
        }
    }
    for(rg int i=1;i<=maxn;i++)mu[i]+=mu[i-1];
}
int solve(int n,int m)
{
    long long ans=0;
    if(n>m)swap(n,m);
    n=n/k,m=m/k;
    for(rg int i=1,j;i<=n;i=j+1)
    {
        j=min(n/(n/i),m/(m/i));
        ans+=1ll*(mu[j]-mu[i-1])*(n/i)*(m/i);
    }
    return ans;
}
int main()
{
    read(n),prepare();
    while(n--)
    {
        read(a),read(b),read(c),read(d),read(k);
        printf("%d\n",solve(b,d)-solve(c-1,b)-solve(a-1,d)+solve(a-1,c-1));
    }
}

转载于:https://www.cnblogs.com/lcxer/p/10242897.html