简介:选择排序是一种基础的排序算法,通过反复选择最小或最大元素并交换位置来逐步完成排序。本篇文章将详细介绍如何使用C语言实现选择排序算法,包括关键步骤和完整代码示例。通过实践这个算法,C语言编程者可以加深对排序过程的理解,提升编程能力。 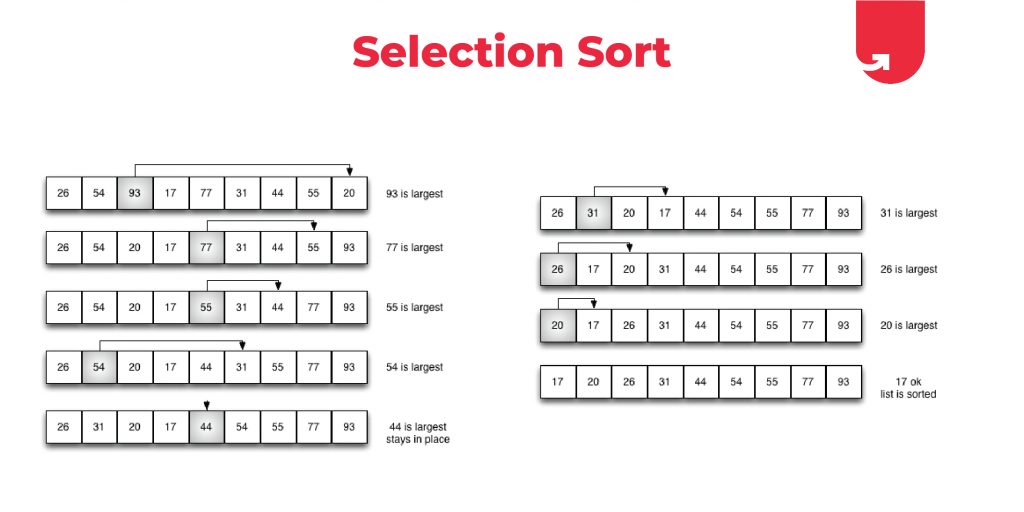
1. 选择排序基础概念和原理
选择排序是计算机科学中一种简单直观的排序算法。基本思想是在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
基本原理
选择排序的原理可以概括为以下几个步骤:
- 初始化 :将数组分为已排序区和未排序区,初始时已排序区为空,未排序区为整个序列。
- 选择操作 :从未排序区选择一个最小(或最大)的元素。
- 交换操作 :将选中的元素与未排序区第一个元素交换位置,这样未排序区的这个元素就归入了已排序区。
- 重复步骤 :重复上述过程,每次从未排序区选择最小(或最大)元素,与未排序区第一个元素交换,直到所有元素排序完成。
这种方法简单直接,但存在时间效率问题,因为每一步都需要进行一次比较和一次交换,总共需要进行 (n-1) + (n-2) + ... + 1 次比较,以及 n-1 次交换(其中 n 为数组元素个数)。尽管如此,选择排序在数据量不大时,由于其代码实现简单,仍然是一个不错的选择。
2. 选择排序的初始化和函数搭建
2.1 初始化选择排序函数
2.1.1 函数定义和参数
选择排序的实现从定义一个基础函数开始。在C语言中,我们可以定义一个名为 selectionSort 的函数,该函数接受一个整型数组和数组的长度作为参数。这样设计的目的是为了能够对任意长度的数组进行排序。数组将被修改为排序后的顺序,因此不需要返回任何值,排序将在原数组上完成。
void selectionSort(int arr[], int n) {
int i, j, min_index;
for (i = 0; i < n-1; i++) {
min_index = i;
for (j = i+1; j < n; j++) {
if (arr[j] < arr[min_index]) {
min_index = j;
}
}
// 交换元素
int temp = arr[min_index];
arr[min_index] = arr[i];
arr[i] = temp;
}
}
参数 arr 是一个指向数组第一个元素的指针,而 n 是数组的长度。函数内部使用两个嵌套循环,外层循环控制排序的轮数,内层循环负责在未排序部分找出最小元素的索引。
2.1.2 排序前后对比
在介绍完基本的函数定义和参数后,可以展示一个简单的例子,用以比较排序前后的数组状态。假设有一个未排序的数组 arr[] = {64, 25, 12, 22, 11} ,通过调用 selectionSort(arr, 5) 后,数组将变为有序状态。
调用前后数组对比如下:
未排序的数组: {64, 25, 12, 22, 11}
排序后的数组: {11, 12, 22, 25, 64}
2.2 函数内部结构搭建
2.2.1 外层循环的框架搭建
在函数的初始版本中,我们需要设置外层循环来迭代数组中的每一元素。由于选择排序是一种不稳定的排序算法,所以外层循环每迭代一次,都会在未排序的部分选出一个最小的元素,然后将其放到已排序部分的末尾。
外层循环的代码如下:
for (int i = 0; i < n - 1; i++) {
// 外层循环的相关逻辑
}
这段代码将外层循环的框架搭建起来,循环中 i 代表当前正在进行排序的轮次,每次循环将处理一个元素,并将其放置在正确的位置。
2.2.2 内层循环的作用和结构
内层循环的主要任务是遍历未排序的部分,并找出最小元素的索引。在找到最小元素后,将其与当前轮次的第一个元素进行交换,从而保证每次循环结束后,未排序部分的最小元素已经被放置到已排序部分的末尾。
内层循环的代码如下:
int min_index = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min_index]) {
min_index = j;
}
}
在这段代码中, min_index 是一个变量,它保存着当前未排序部分最小元素的索引。通过比较所有未排序的元素,我们不断更新 min_index ,直到内层循环结束,找到最小元素为止。
内层循环结束后,执行元素交换操作,确保最小元素被移动到已排序部分的末尾。这个过程会一直重复,直到数组完全有序。
3. 选择排序核心算法实现
3.1 实现外层循环控制
3.1.1 控制排序次数和起始点
选择排序的基本思想是通过一系列的循环,每次从未排序的数组部分选出最小(或最大)的元素,然后将其放置在已排序序列的末尾。在实现上,我们需要一个外层循环来控制排序的总次数。假设我们有一个数组 arr,大小为 n,我们只需要进行 n-1 轮排序,因为在每一轮排序后,都会有一个元素被放置在它的最终位置。
for (int i = 0; i < n - 1; i++) {
// 外层循环控制
}
在外层循环中,变量 i 代表当前的轮数,它从 0 开始,到 n-2 结束。每一轮都会找到未排序部分的最小元素,并将其与未排序部分的第一个元素交换。
3.1.2 外层循环逻辑分析
外层循环是整个选择排序的核心,它确保了所有的元素都将被排序。在每次循环的开始,我们假设当前未排序部分的第一个元素是最小的。随后,内层循环将负责找到真正的最小元素。
为了帮助理解,我们可以将排序过程可视化为一系列步骤:
- 外层循环开始,假设第一个元素是最小的。
- 内层循环开始遍历剩余的元素。
- 内层循环找到最小元素后,将其与外层循环的当前元素交换。
- 外层循环结束时,已排序部分的最后一个元素是整个未排序数组中的最小元素。
3.2 实现内层循环寻找最小值索引
3.2.1 内层循环的起始点和终止条件
内层循环负责在未排序的部分寻找最小元素。它的起始点是外层循环的当前索引加一,因为每次外层循环迭代后,前一个索引的元素已经被放置在了其最终位置。终止条件是内层循环到达未排序部分的末尾。
for (int j = i + 1; j < n; j++) {
// 内层循环寻找最小值索引
}
在这段代码中, j 是内层循环的变量,它从外层循环的当前索引 i 加一开始,直到数组的末尾。
3.2.2 寻找最小值索引的方法
为了找到最小值的索引,我们需要比较当前已知的最小值与未排序部分的每个元素。我们通常使用一个变量 minIndex 来跟踪最小值的索引。在内层循环的每次迭代中,如果发现比当前已知的最小值更小的元素,就更新 minIndex 。
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
在内层循环结束后, minIndex 将指向未排序部分最小元素的索引。接下来,我们通过交换将这个元素移动到已排序部分的末尾。
3.3 实现元素交换逻辑
3.3.1 元素交换的必要性
元素交换是选择排序中非常关键的步骤。它确保了每次外层循环迭代结束时,未排序部分的最小元素会被放置在已排序部分的正确位置。如果没有元素交换,我们就无法将最小元素移动到正确的位置,排序就会失败。
3.3.2 交换逻辑的实现方法
在C语言中,我们可以使用一个临时变量来帮助我们完成交换。以下是交换两个变量的值的典型方式:
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
在选择排序的上下文中,我们使用这个 swap 函数来交换外层循环当前索引 i 的元素和找到的最小元素 minIndex 的值。
swap(&arr[i], &arr[minIndex]);
通过这种方式,我们可以确保在每轮排序结束时,数组中的一部分已经正确排序。在所有轮次的排序完成后,整个数组也就被完全排序了。
4. 选择排序C语言代码实践
选择排序算法的C语言实现需要对每个细节都有深入的理解,这包括如何在代码层面组织循环结构,如何交换数组元素,以及如何进行调试以确保算法的正确性。本章将带领读者通过实践的方式深入探索选择排序的代码实现。
4.1 完整选择排序代码框架
在编写完整的C语言选择排序代码之前,需要先构建一个清晰的代码框架。这需要定义一个排序函数,并明确其参数和返回值。然后,按照选择排序的逻辑,逐步完善函数内部的各个部分。
4.1.1 函数整合和代码结构
选择排序的实现可以分解为以下几个关键部分:
- 定义排序函数,输入参数是待排序数组和数组的长度。
- 构建外层循环,用于控制排序的总次数。
- 构建内层循环,用于每次从剩余未排序部分找出最小元素的索引。
- 实现元素交换逻辑,当找到最小元素后,与当前未排序部分的第一个元素交换。
下面是选择排序的C语言实现的代码框架,包含必要的注释:
#include <stdio.h>
// 函数声明
void selectionSort(int arr[], int n);
int main() {
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
printf("Sorted array: \n");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
// 选择排序实现
void selectionSort(int arr[], int n) {
int i, j, min_idx;
// 外层循环遍历数组的每个元素作为基准
for (i = 0; i < n-1; i++) {
// 找到从i到n-1中的最小元素索引
min_idx = i;
for (j = i+1; j < n; j++) {
// 如果找到更小的元素,则更新最小索引
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// 将找到的最小元素与i位置的元素交换
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
4.1.2 代码注释和逻辑清晰化
代码注释是代码清晰化的重要部分。它帮助读者理解代码的功能,特别是复杂的算法实现。在上述代码中,注释被放置在关键部分,以解释每一步的目的。
// 外层循环遍历数组的每个元素作为基准
for (i = 0; i < n-1; i++) {
// 找到从i到n-1中的最小元素索引
min_idx = i;
for (j = i+1; j < n; j++) {
// 如果找到更小的元素,则更新最小索引
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// 将找到的最小元素与i位置的元素交换
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
4.1.3 代码执行逻辑分析
在执行时,选择排序的外层循环负责逐个确定基准元素,内层循环则用于寻找该基准元素右侧最小的元素。找到最小元素后,通过一个临时变量 temp 与基准元素交换,以达到排序的目的。
每一行代码都有明确的目的,并且通过注释进行了说明。这样的代码结构有助于阅读和维护,同时也能清晰地反映算法的逻辑。
4.2 排序功能测试与调试
为了确保排序函数的正确性,必须进行充分的测试和调试。这包括选择合适的测试数据集,并在调试过程中识别和修正可能出现的问题。
4.2.1 测试数据的选择和预设
选择具有代表性的测试数据是测试过程中的第一步。为了测试选择排序,可以设计以下几种测试用例:
- 已排序的数据
- 逆序排列的数据
- 随机排列的数据
- 包含重复元素的数据
通过这些测试用例,可以全面地验证排序算法在不同情况下的表现和正确性。
4.2.2 调试过程和常见问题解决
调试是程序开发过程中不可或缺的一部分。在调试选择排序时,可能会遇到的问题有:
- 循环条件错误 :确保循环的起始条件和终止条件正确无误。
- 数组边界问题 :正确处理数组的起始和结束索引,避免越界访问。
- 交换逻辑错误 :在交换元素时确保使用临时变量正确无误。
为了调试这些潜在问题,可以使用IDE(集成开发环境)的调试工具,设置断点来逐步执行程序,并查看变量的值以及程序的执行流程。如果出现问题,IDE的调试信息和输出结果将帮助快速定位问题所在。
在开发选择排序算法时,务必确保每一步逻辑都被正确地执行,并通过不断的测试和调试来验证结果。这样不仅可以提高代码的可靠性,还能深入理解算法的工作原理。
4.2.3 常见问题及代码示例
为了确保选择排序算法的正确性,下面列出了一个常见问题及其代码示例,以供参考:
- 问题 : 选择排序算法在处理数组时可能会越界。
- 代码示例 :
// 注意此处的内层循环起始条件应为 i+1
for (j = i+1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
- 分析 : 在内层循环中,起始条件设置为
i+1而不是i,这是为了确保每次只比较未排序部分的元素。这避免了不必要的比较,并防止了潜在的越界问题。如果起始条件设置为i,则会导致与已排序部分的第一个元素比较,这不仅浪费时间,也可能引起数组越界。
在实际开发过程中,编写测试用例并进行调试是验证程序正确性的关键步骤。通过上述示例,可以对选择排序中的潜在问题有所了解,并采取相应的措施来避免错误。
5. 选择排序的优化与进阶应用
在上一章我们完成了选择排序的C语言代码实现,本章将深入探讨选择排序的优化策略,分析其时间复杂度,并讨论选择排序在实际项目中的应用情况。
5.1 选择排序的时间复杂度分析
选择排序算法的时间复杂度分析是衡量其性能的重要指标。让我们逐步深入理解。
5.1.1 算法效率的评估
选择排序算法的主要步骤包括:
- 从未排序序列中选出最小(或最大)元素。
- 将其与未排序序列的第一个元素交换位置(如果起始序列为升序排序)。
- 重新从剩余未排序元素中继续这个过程,直到所有元素均排序完毕。
对于含有 n 个元素的数组,选择排序的比较次数为 C(n) = n * (n - 1) / 2 ,因此其时间复杂度为 O(n^2) 。这一结果表明,选择排序的效率并不高,尤其是在数据量较大的情况下。
5.1.2 与其他排序算法的比较
与快速排序、归并排序等 O(n log n) 级别的时间复杂度排序算法相比,选择排序在效率上不占优势。然而,选择排序有其优点,如原地排序(不需要额外的存储空间),且算法的交换次数较少。
5.2 选择排序的优化策略
由于选择排序本身的时间复杂度限制,优化策略主要集中在提高算法的稳定性和减少不必要的比较上。
5.2.1 算法优化的可能性和方向
- 减少比较次数 :可以考虑在每次选择最小元素时,就对剩余元素进行比较,并更新最小元素的位置。
- 稳定性的提升 :在某些应用场景中,保持相等元素的相对顺序是有用的。选择排序本身不是稳定的排序,但可以通过一些改进使其成为稳定排序。
- 早停策略 :如果在一次遍历中发现数组已经是有序的,那么排序可以提前结束。
5.2.2 具体优化实例和效果展示
以下是选择排序的一个优化版本,其中加入了早停策略以减少不必要的迭代:
void optimizedSelectionSort(int arr[], int size) {
for (int i = 0; i < size - 1; i++) {
int min_idx = i;
for (int j = i + 1; j < size; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
if (min_idx != i) {
// 交换操作
int temp = arr[i];
arr[i] = arr[min_idx];
arr[min_idx] = temp;
} else {
// 已排序,提前终止循环
break;
}
}
}
这个改进的版本在数组已经排序时能够提前停止排序,从而节省时间和计算资源。
5.3 选择排序在实际项目中的应用
在现实的项目中,选择排序并不是最优的排序算法,但依然有它的用武之地。
5.3.1 应用场景分析
选择排序适用于数据量较小的场景,例如在一个小型系统中对数据进行简单排序。另外,由于选择排序的代码实现较为简洁,因此在教育中通常作为排序算法教学的入门案例。
5.3.2 实际代码案例和效果评估
假设我们需要在一个简单的管理系统中对用户ID进行排序,由于数据量不多,我们可以使用选择排序:
#include <stdio.h>
// ...(此处省略了优化选择排序函数的代码)
int main() {
int userIDs[] = {34, 24, 12, 56, 78, 90, 12};
int n = sizeof(userIDs) / sizeof(userIDs[0]);
optimizedSelectionSort(userIDs, n);
printf("Sorted IDs: ");
for (int i = 0; i < n; i++) {
printf("%d ", userIDs[i]);
}
printf("\n");
return 0;
}
执行上述代码,用户ID将被排序。在实际应用中,选择排序可以满足需求并保持代码简洁。
选择排序可能不是最优的排序方法,但它在特定情况下依然有其应用价值。在优化选择排序以提高效率的同时,我们也要清楚地认识到其时间复杂度的局限性,并在适合的场景中使用它。
简介:选择排序是一种基础的排序算法,通过反复选择最小或最大元素并交换位置来逐步完成排序。本篇文章将详细介绍如何使用C语言实现选择排序算法,包括关键步骤和完整代码示例。通过实践这个算法,C语言编程者可以加深对排序过程的理解,提升编程能力。





















 186
186

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








