Largest Rectangle in a Histogram（hdu1506，单调栈裸题）

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 22968    Accepted Submission(s): 7175

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

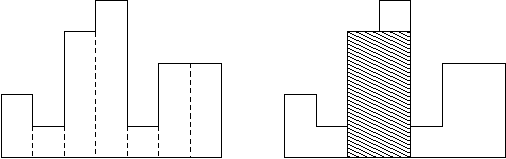
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

 

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

 

 

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

 

 

Sample Input

7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0

 

 

Sample Output

8 4000

 

 

Source

University of Ulm Local Contest 2003

 

 

Recommend

LL   |   We have carefully selected several similar problems for you:   1505  1069  1087  1058  1176 

 

思路：

感觉太裸了点

还是单调栈，这回是个单调递增栈

因为如果以当前这个高度作为矩形的高度的话后面的矩形高度必须比他高

否则就不成立

那么我们维护一个单调递增栈

当他需要被弹出时，则说明以该高度为高的矩形走不下去了

那么我们就可以记下端点

记得正反跑两遍

最后用（右端点-左端点+1）*高度就是当前矩形面积

取max即可

（别忘了开long long）

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define rii register int i
#define rij register int j
#define int long long
using namespace std;
int l[100005],r[100005],h[100005],n,cnt,stack[100005];
signed main()
{
    while(~scanf("%lld",&n))
    {
        if(n==0)
        {
            break;
        }
        for(rii=1;i<=n;i++)
        {
            scanf("%lld",&h[i]);
        }
        cnt=0;
        for(rii=1;i<=n;i++)
        {
            if(cnt==0)
            {
                cnt++;
                stack[cnt]=i;
                continue;
            }
            if(h[stack[cnt]]<=h[i])
            {
                cnt++;
                stack[cnt]=i;
            }
            else
            {
                while(h[stack[cnt]]>h[i])
                {
                    r[stack[cnt]]=i-1;
                    cnt--;
                }
                cnt++;
                stack[cnt]=i;
            }
        }
        while(cnt!=0)
        {
            r[stack[cnt]]=n;
            cnt--;
        }
        for(rii=n;i>=1;i--)
        {
            if(cnt==0)
            {
                cnt++;
                stack[cnt]=i;
                continue;
            }
            if(h[stack[cnt]]<=h[i])
            {
                cnt++;
                stack[cnt]=i;
            }
            else
            {
                while(h[stack[cnt]]>h[i])
                {
                    l[stack[cnt]]=i+1;
                    cnt--;
                }
                cnt++;
                stack[cnt]=i;
            }
        }
        while(cnt!=0)
        {
            l[stack[cnt]]=1;
            cnt--;
        }
        int ans=0;
        for(rii=1;i<=n;i++)
        {
            ans=max(ans,(r[i]-l[i]+1)*h[i]);
        }
        printf("%lld\n",ans);
    }
}

 

转载于:https://www.cnblogs.com/ztz11/p/9699712.html