简述递归和分治的关系_漫画：到底什么是分治算法？和递归有什么关系？

欢迎关注微信公众号：视学算法，后台回复【学习】获取5T程序员全栈资料。

分治顾名思义“分而治之”，英文的意思翻译为“分割并征服”。

分治思想，简而言之就是将原问题分解成与“原问题相同但是规模更小”的子问题，并可以反复执行这个过程，使得问题规模减小到可以求解为止。

1、快速排序算法

2、快速傅里叶变换算法

3、Karatsuba大数乘法算法

问题：给定1000个数，从小到大进行排序。

先选择一个“标准”A，按照“比A小”和“比A大”将原来的数列分为两类，这样，只需要将两个子序列分别排好序，然后再合并到一块就ok了。

直接做该运算，需要做平方级别的复数乘法，这样的复杂度超级高！如何进行分解呢？

首先，不可能像上边排序算法一样，找一个“标准数”，取前一半和后一半采样点来做！

问题：两个很大的数相乘，如何更快的解决？

两个很大的数相乘，普通算法的时间复杂度为O(n^2)。

首先，将n位大数x和y进行分解。

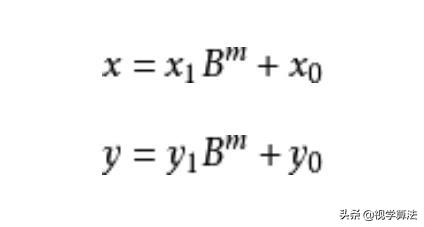
然后，x·y就变成了下面这样

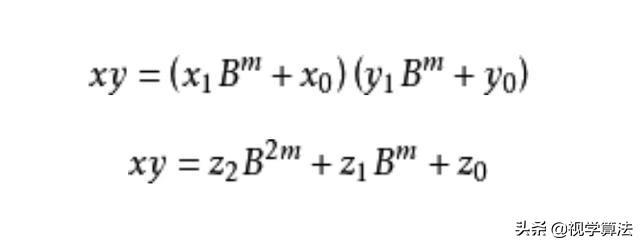
并且满足

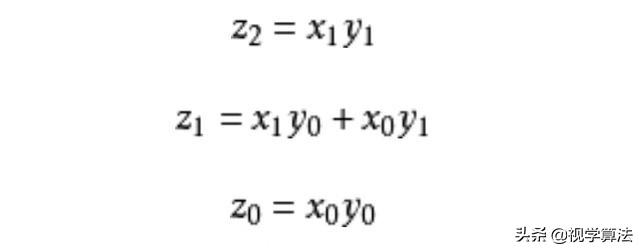
所以，原来的大数乘法就变成了小数乘法！其实这位博士研究的算法不仅这里巧妙，而且还有一个小技巧！

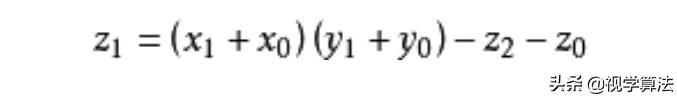
这样的话，乘法又能变成加法了！计算复杂度又大大的降低了！

第一：数学归纳是使用分治思想

只要出现可以用数学归纳公式来表示的大规模问题，第一反应就应该想到分治算法，通过特定的函数参数安排，一定可以用同一个函数来表述不同规模的问题，套用递归结构，可迅速解决问题！

第二：分治思想不一定使用递归结构

递归结构是循环结构的一种，也是分治思想应用最多的一种程序结构，但是不一定要使用它！关键在于能够写出递归公式以及是否有必要使用递归算法。比如上边提到的快速傅里叶变换算法，就没有用到递归！

三：分治思想的核心是“如何分”

能够把问题很棒的进行分解，也是一种能力和本事！也就是说把问题用分治法来进行解决，是算法的难点，也是重点！一方面需要经验，另一方面也需要想象力！所以说呢？人生也是如此！不管遇到多大的苦难，我们需要在一次一次的锻炼中进行学会分解苦难，才能够大事化小，小事化了！

欢迎关注微信公众号：视学算法，后台回复【学习】获取5T程序员全栈资料。