填格子3N的方框使用21的矩形进行填充

最新推荐文章于 2024-10-28 17:50:03 发布

weixin_30795127

最新推荐文章于 2024-10-28 17:50:03 发布

阅读量489

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Opaser/p/4444478.html

本文介绍了一种利用矩阵快速幂技术优化动态规划问题的方法。通过实例代码展示了如何将状态转移过程转化为矩阵乘法，并利用快速幂加速计算，特别适用于周期性或规律性的状态转移场景。

考虑每个位置的前一个状态可以发现有

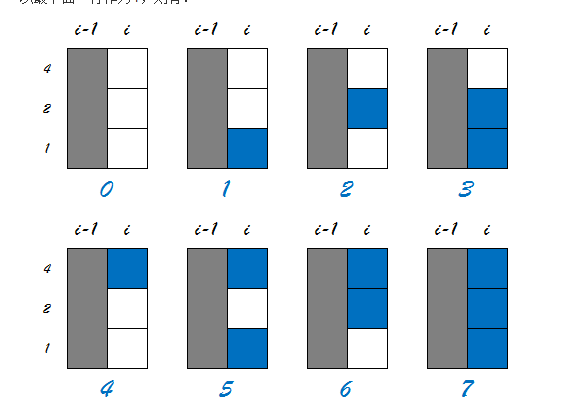
我们分别给他们编号假设现在填充到了i+1行，我们可以发现从i行可以通过填充转到i+1行的状态

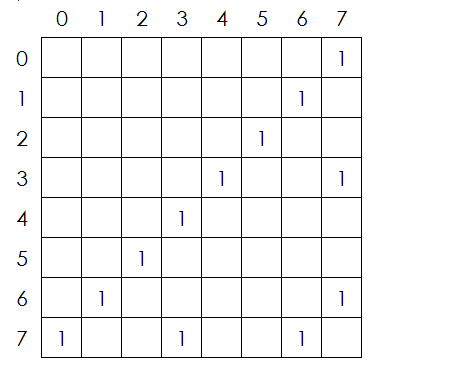
第i行第j列表示可以从上一个转态 j 可以到达这个状态的j ，然后又了这个转态转化在使用矩阵

{00000001}为初始状态

#include <iostream>
#include <algorithm>
#include <string.h>
#include <vector>
#include <cstdio>
using namespace std;
typedef long long LL;
const LL mod=12357;
struct Matir{
   LL va[8][8];
   Matir(){
       memset(va,0,sizeof(va));
   }
   Matir operator *(const Matir rhs){
      Matir ans;
         for(int i=0; i<8; i++)
         for(int j=0; j<8; j++){
                 for(int k=0; k<8; k++){
                   ans.va[i][j]=(ans.va[i][j]+(va[i][k]*rhs.va[k][j])%mod )%mod;
                 }
         }
         return ans;
   }
}model;
Matir solve(int N){
     Matir ans;
     for(int i=0; i<8; i++)ans.va[i][i]=1;
     Matir A=model;
     while(N){
        if(N&1)ans=ans*A;
        N>>=1;
        A=A*A;
     }
     return ans;
}
int main()
{
    for(int i=0; i<8; i++)
        model.va[i][8-i-1]=1;
        model.va[3][7]=1; model.va[6][7]=1; model.va[7][3]=1;model.va[7][6]=1;
      int N;
      while(scanf("%d",&N)==1){
          if(N&1){
             printf("0\n");continue;
          }
          Matir ans=solve(N);
          cout<<ans.va[7][7]<<endl;
      }
    return 0;
}