机器学习基石第六讲 Theory of Generalization

一.Restriction of Break Point

 

 

 

shatter两个点就是取到两个点的所有情况。

 

 

 

 

 

不满足k = 2

 

 

 

 

 

 

 

 

 

如果任意再加进去一组，那么肯定破坏了k=1.

 

二.Bounding Function: Basic Cases

任意k个点都不存在shatter

 

 

 

 

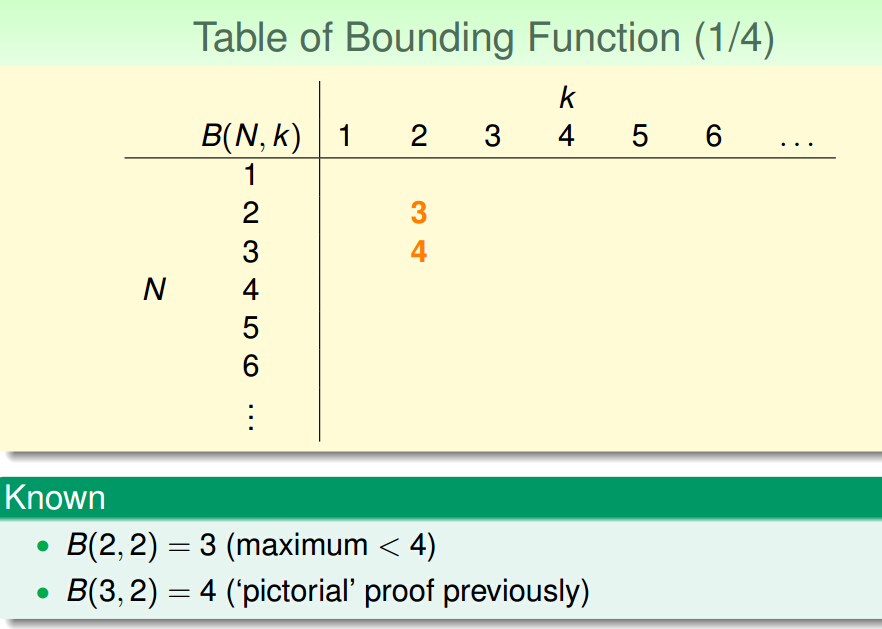
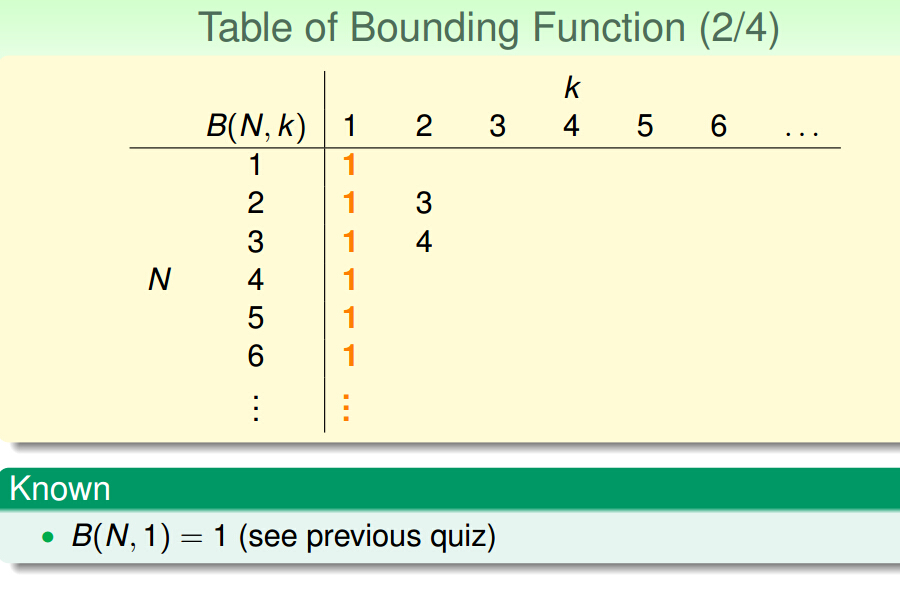
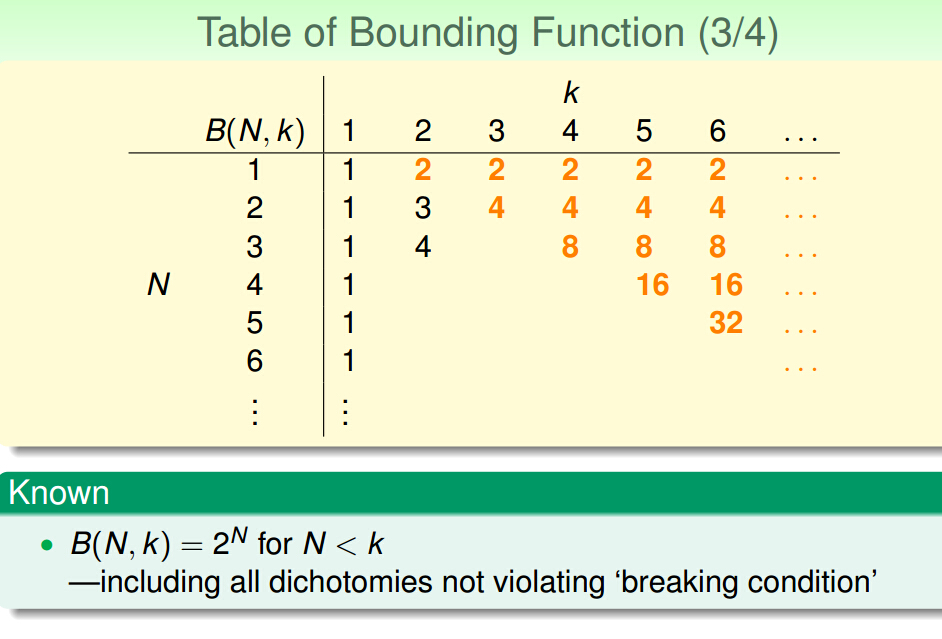
三.Bounding Function: Inductive Cases

建立B(4,3)和B(3,?)之间的联系

 

 

 

 

 

 

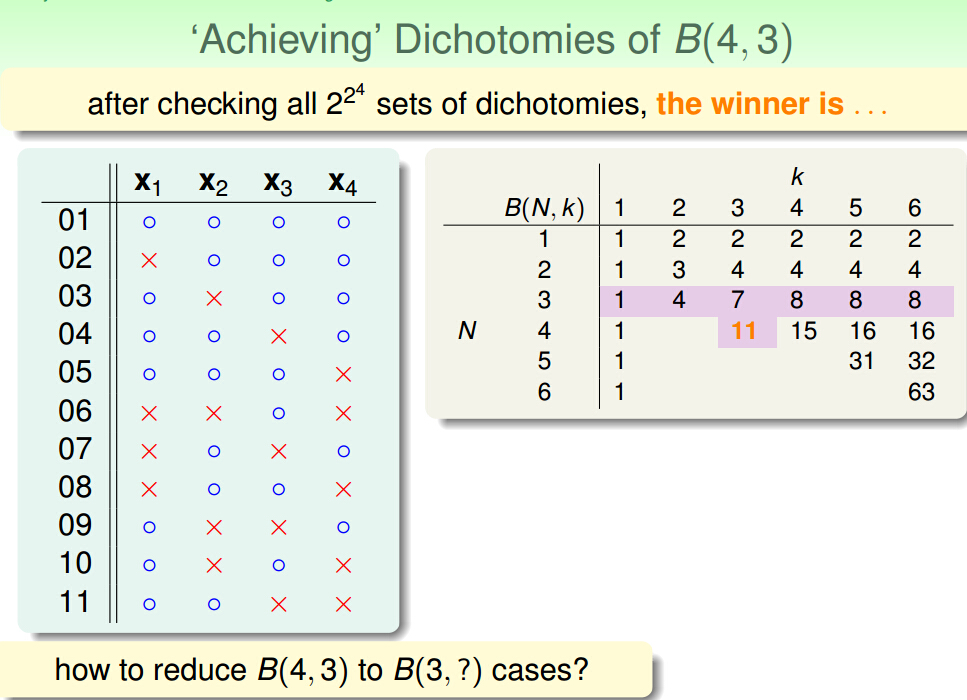
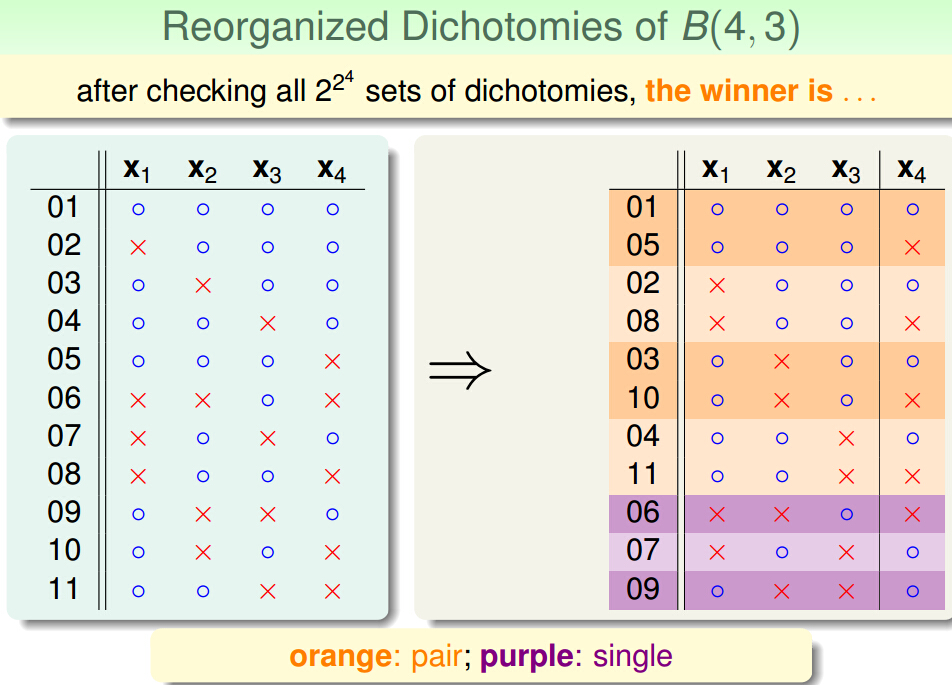
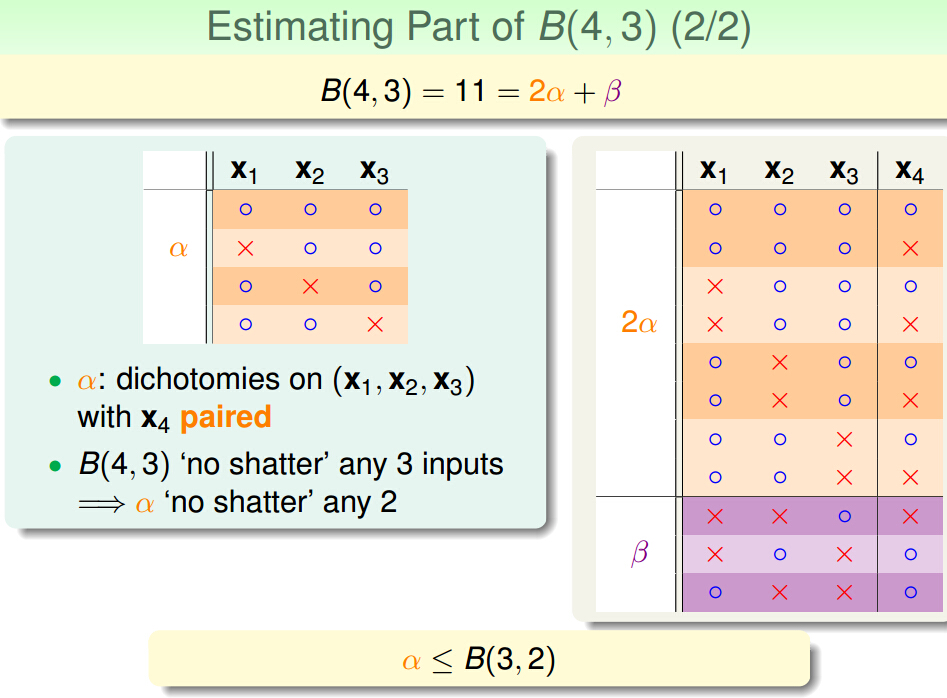
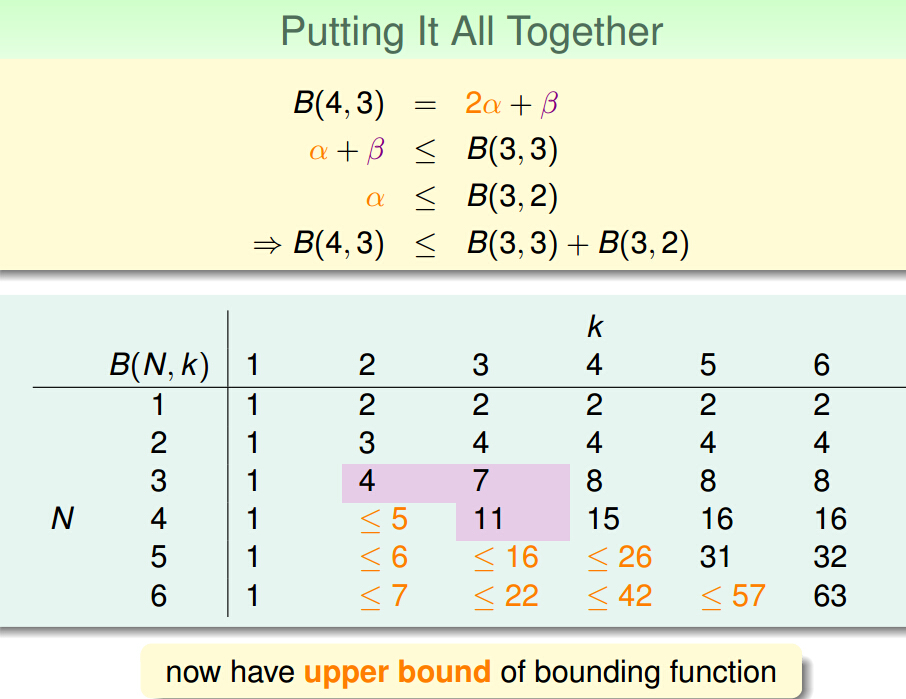
回顾一下，将B(N,K)拆成2a+b，a+b在x1~xn-1这一部分，满足B(N-1,K)所以a+b ≤ B(N-1,K)，剩下的a在

 

x1~xn-1中肯定不存在任意k-1个点shatter，不然在2a中这k-1个shatter的点加上xn之后，就形成了k个shatter的点

 

所以a ≤ B(N-1,K - 1) => B(N,K) ≤ B(N - 1,K) + B(N - 1,K - 1)

 

 

 

数学归纳法：

 

 

 

四.A Pictorial Proof

 

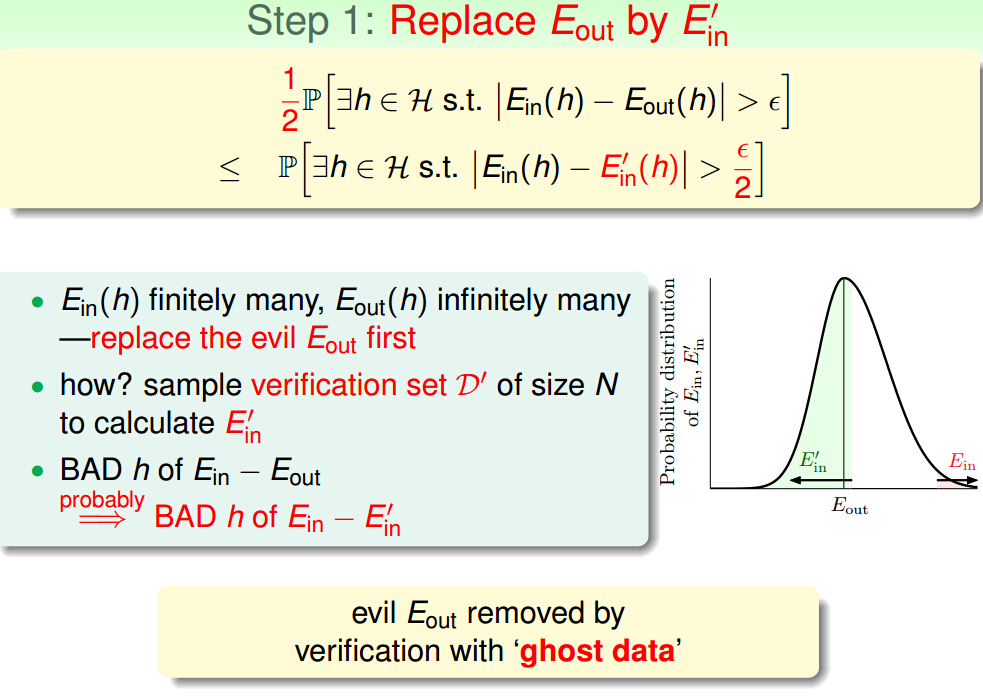
在这个图我们可以看出Ein和Eout里的很远的时候，我们起码有1/2的概率选择的E'in也和Ein离得很远，其实肯定不止1/2这个数

 

 

 

 

 

 

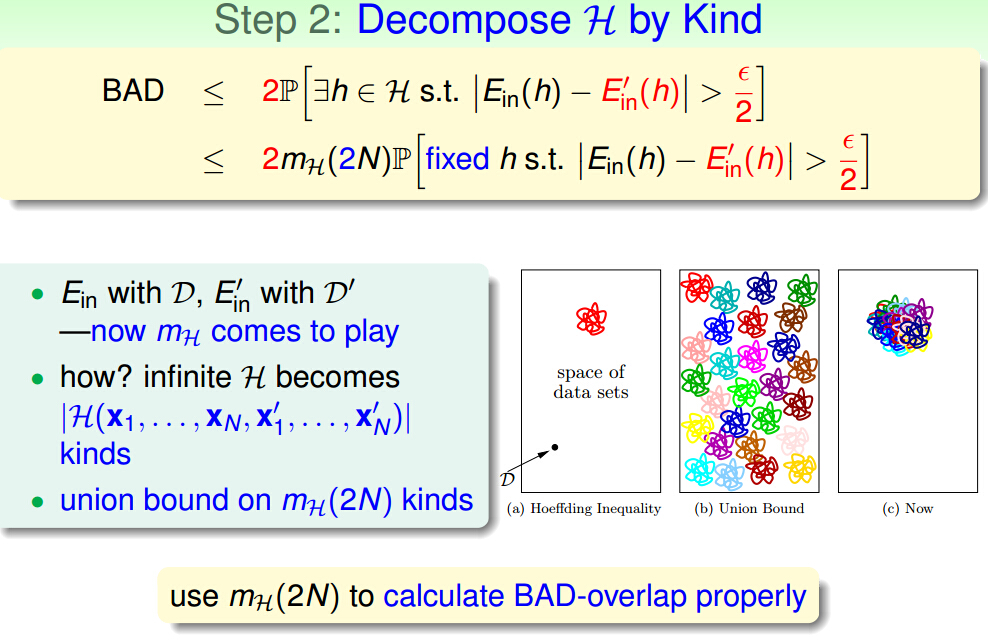
 Eout可能是无限多种情况，所以这里我们要用E‘in替代Eout，取2N个sample，一半是Ein，一半是E'in

 

改成E'in后条件要严格一点所以改成ξ/2，|Ein - E'in| > ξ/2，再改为对2N取平均：|Ein - （Ein + E'in）/ 2| > ξ/4

 

综合上述所有条件就得到了公式。

 

 

转载于:https://www.cnblogs.com/wanderingzj/p/4967052.html