[Algorithm] Fibonacci problem by using Dynamic programming

最新推荐文章于 2025-08-20 15:37:55 发布

转载最新推荐文章于 2025-08-20 15:37:55 发布 · 70 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Answer1215/p/10366741.html

文章标签：

#python

本文探讨了解决斐波那契数列问题的三种方法：递归、带备忘录的递归（记忆化）和自底向上（动态规划）。详细分析了每种方法的时间复杂度，指出自底向上方法在处理大规模问题时更为高效。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

vThere are three ways to solve Fibonacci problem

Recursion
Memoize
Bottom-up

'First Recursion approach:

def fib(n):
    if n == 1 or n == 2:
        result = 1
    else:
        result = fib(n-1) + fib(n -2)
    
    return result;

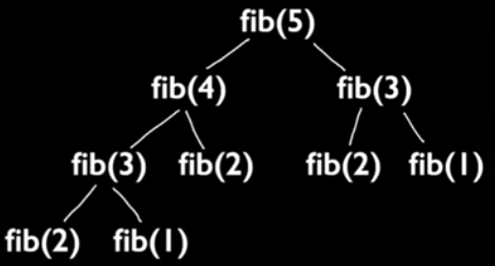
As we can see to calculate fib(5), we need to calculate fib(3) twice and fib(2) three times.

Time complexity is O(2^n), because for each n from 3, we need to call fib() twice in else block:

else:
    result = fib(n-1) + fib(n -2)

To solve the problem, we can use memoize solution to solve repeated calculation.

deb fib(n, memo):
    if memo[n] != null
        return memo[n]
    if n == 1 or n == 2:
        result = 1
    else:
        result = fib(n - 1) + fib(n-2)
    memo[n] = result
    return result

Using fib(5) as example: to calulate fib(5) we need to know fib(4)..fib(3), fib(2), fib(1), since we already know fib(1), fib(2) = 1, then we can know fib(3) = 2..fib(4) = 3, fib(5) = 5.

Time complexity is O(2n + 1) -> O(n): because we just need to go though memo once. And 2*2 is because of:

result = fib(n - 1) + fib(n-2)

We still can improve it by using bottom up approach, because from the previous solution:

Using fib(5) as example: to calulate fib(5) we need to know fib(4)..fib(3), fib(2), fib(1), since we already know fib(1), fib(2) = 1, then we can know fib(3) = 2..fib(4) = 3, fib(5) = 5.

We can clear see the solution the problem by going from bottom (fib(1) & fib(2)) to up (fib(5)):

def fib_bottom_up(n):
    if n == 1 or n == 2:
        return 1
    bottom_up = new int[n+1]
    bottom_up[1] = 1
    bottom_up[2] = 1
    for i from 3 upto n:
        bottom_up[i] = bottom_up[i-1]+bottom_up[i-2]

    return bottom_up[n]

Time complexity is O(n).

Notice that some programming language has recursion limit, for example, python has set the limiation to 1000, which mean if you keep calling one function 1000 times, it will throw errors.

In this sense, bottom up is much better than recursion apporach (recursion and memoize).

转载于:https://www.cnblogs.com/Answer1215/p/10366741.html