三因素方差分析_医学统计之多元回归分析（三）

医学统计之多元回归分析

一、多元线性回归相关介绍

在医学统计领域，变量之间的关系常常是需要进行分析的。如血压值与年龄、性别的关系；身高与饮食习惯、年龄的关系；肿瘤预后与救治方法、肿瘤种类的关系等。对于这类变量之间关系的研究可采取回归分析来完成，对每个因素做出相应的评价，同时，回归分析还可以用来对预测和判别。其中，回归分析可分为一元线性回归和多元线性回归，一元线性回归研究的是一个因变量与单个自变量之间的关系；多元线性回归研究的是一个因变量与多个自变量间的关系，从实用意义上看，多元线性回归优于一元线性回归。

PS:多元线性回归的模型结构为:β₀+β₁x₁+…+β_kx_k+ε

多元线性回归的预测模型为：`Y= b₀+ b₁x1+…+b_kx_k

其中Y表示任意的数值变量，β₀、β₁、β_k称为偏回归系数，这些偏回归系数的估计值b₀、b₁、b_k是采用最小二乘法获得。

二、实例分析

     本文随机选取了某院27名糖尿病人，并测量了其各自的血清总胆固醇、甘油三脂、空腹胰岛素、糖化血红蛋白和空腹血糖值，旨在研究空腹血糖与其他几个指标的关系。具体操作如下所示。

样本数据：

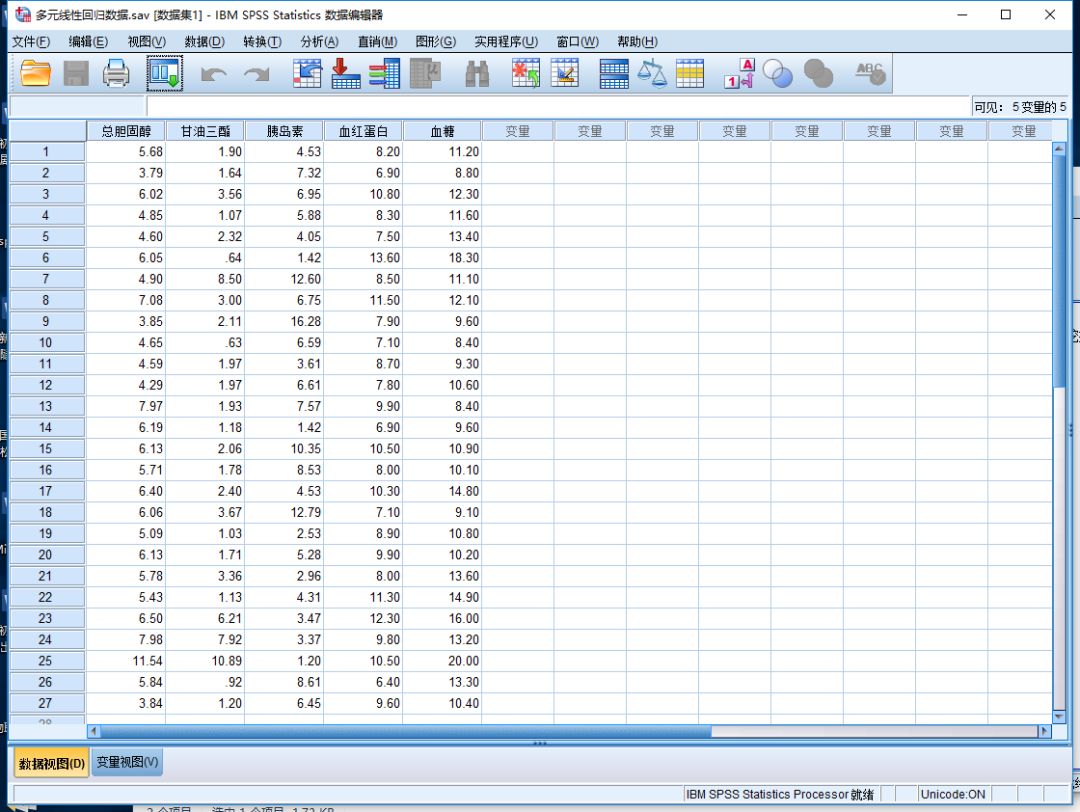
步骤指导：

【1】将数据导入spss22.0中→【2】点击“分析”→【3】点击“回归”→【4】点击“线性回归”→【5】将“血糖”导入因变量栏中，将其余值导入自变量栏中→【6】点击“确定”。结果如下图所示。

1、结果描述

     从【输出表一】可以看出，决定系数R²为0.601，校正系数R²为0.52，此外，决定系数的大小可以说明回归方程的拟合程度，越大说明越好，反之越差;【输出表二】是对模型作的方差分析， F为8.28，显著性小于0.001，说明该回归模型有统计学意义;【输出表三】是回归方程的参数估计和统计学检验，非标准系数包括B偏回归系数和标准误。可以根据该输出表写出回归方程：血糖=5.943+0.142总胆固醇+0.351甘油三脂-0.271胰岛素+0.638血红蛋白。可以看出总胆固醇的显著性为0.701，甘油三脂的显著性为0.099，均大于0.05，因此说明其回归系数无统计学意义。胰岛素和血红 蛋白的显著性分别为0.036、0.016，均小于0.05，因此说明 其回归系数有统计学意义。即，即胰岛素和血红蛋白影响空腹血糖水平。

三、多元逐步线性回归

     同样采用上文数据，多元逐步线性回归的操作步骤为：【1】将数据导入spss22.0中→【2】点击“分析”→【3】点击“回归”→【4】点击“线性回归”→【5】将“血糖”导入因变量栏中，将其余值导入自变量栏中→【6】在方法栏中选择“逐步”，如下图所示，而后点击确定即可。通过此番操作旨在筛选出不会对因变量造成影响的自变量。

结果显示：

2、结果描述

注意事项：

结果显示：

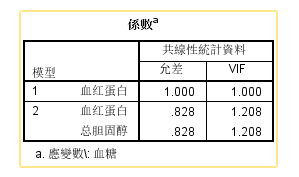
3、结果描述

    【输出表一】可以看出，血红蛋白和总胆固醇的容忍度均为0.828，方差膨胀因子均为1.208。容忍度是以每个自变量作为因变量，对其他自变量进行回归分析时得到的残差比例，可由1-定系数来表示。该指标越小，说明该自变量被其余自变量预测的越精确，共线性就越严重。方差膨胀因子是容忍度的倒数，该值越大，说明共线性越严重。 由此可以认为案例中的自变量间不存在共线性。【输出表二】可以看出第二个模型的第一维度的特征值为2.944，其余3个维度的条件指数均小于30，因此可以认为本例中自变量间不存在共线性。

PS：判断自变量间可能存在共线性的前提条件是要有大于30的维度的条件指数

四、小结

     在作回归分析时，可忽略那些无法影响因变量的自变量，这样不但能减少计算量，而且还能提高计算的精确度。故，要适当选取需要的研究变量，建立较优的回归模型。若出现多重共线性的问题，可采取以下措施来解决多重共线性的问题，第一，增大样本含量；第二，剔除不重要的解释变量；第三，进行主成分分析等。

再会！！！

好啦，本期的讲解就到此结束啦，感谢大家浏览，我们下期见~

腾讯课堂：泞露专案分析免费课堂：https://ke.qq.com/course/350356?
tuin=119f8c8a
叁藏科研平台联合泞露文化发布

科研就像一场旅行，有人指引你，你不必担心前方的路

叁藏【D2导师】陪你一起完成科研旅行