贪心算法

最新推荐文章于 2020-11-08 23:47:24 发布

转载最新推荐文章于 2020-11-08 23:47:24 发布 · 310 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/qiusuo/p/5231045.html

文章标签：

#数据结构与算法

本文讨论了使用贪心算法解决活动选择问题的方法，包括活动选择算法的递归实现，贪心算法的原理，以及赫夫曼编码在最优编码树构建中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

有n个任务，每个任务ai有一个开始时间si和结束时间fi，在一个时间段内，最多能够进行进行的活动次数。

使用贪心算法，最早结束的活动结束后剩余的时间，才能被尽可能多的活动使用。所以贪心算法只需要不断需找最早结束的活动。

RecurisiveActivitySelector(s,f,k,n)
{
    m=k+1
    while(m<=n && s[m]<f[k])
        m++;
    if(m<=n)
        return {a[m]}UArcurisiveActivitySelector(s,f,m,n)
    else
        return null;
}

贪心算法原理

每一次选择，不依赖后边的选择。
具有最优子结构。

赫夫曼编码

对于字符序列，假设其中出现6个字符

定长编码：使用3个二进制位区分这些字符，每个字符用定长的三个二进制位表示。
变长编码：高频字符用短码，低频字符用长码。

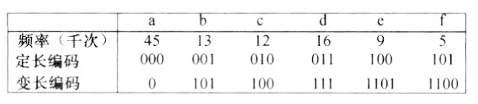
这两种编码对应的查找方法，对应于两种编码树

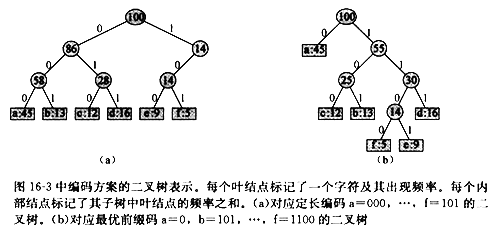
文件的最优编码总是对应一个满二叉树。对于一个编码树T，根据字符出现的次数，可以计算出编码树的代价。

B(T) = P(c1)*L(c1)+P(c2)*L(c2)+...+P(cn)*L(cn)，其中P(cn)和L(cn)表示字符cn出现的频率和编码长度。

赫夫曼编码

赫夫曼编码就是一种构造最优编码树的方法。使用的是贪心算法。

Huffman(C)
{
    n=C.Count;
    MinQueen Q=new MinQueen(C);
    for(i=1..n-1)
        node z;
        z.left=x=Q.ExtractMin()//去除队列最小频率节点，返回
        z.right=y=Q.ExtractMin()//去除队列最小频率节点，返回
        z.freq=x.freq+y.freq;
        Q.insert(z);
    return Q.ExtractMin();
}

转载于:https://www.cnblogs.com/qiusuo/p/5231045.html