# P5629 【AFOI-19】区间与除法
## 题目背景
SY 好不容易才解出QM给她的数学题,在恰午饭的时候,QM 向她的脑洞里塞了个幻想的泡泡……SY 戳开一看,又是长长的一串数字!
SY 实在是不想思考了,她决定用小学的除法消灭她脑洞里的数字.
## 题目描述
定义 $op$ 操作意义为将当前数除以 $d$ 并向下取整.
SY 现在有 $m$ 个“原数”,若一个数经过若干次 $op$ 操作(包括 $0$ 次)后能变为这个“原数”,那么这个数是可以被这个“原数”所消灭的。注意,“原数”是不会被消耗的.
现在 SY 想问你,对于一个区间 $[l,r]$,在消灭最多个数的前提下最少需要多少个“原数”?
## 输入格式
第一行 $4$ 个数,分别是 $n,m,d,q$,分别表示数列 $\{a\}$ 元素个数,SY 拥有的 “原数” 个数,$op$ 操作参数,询问个数。
第二行为 $\{a\}$ 数列,即需要被消灭的数列。
第三行为 $m$ 个“原数”。
接下来 $q$ 行,每行两个数 $l$ 和 $r$,表示询问区间为 $[l,r]$。
## 输出格式
按照询问顺序,每一行输出一个整数表示答案.
## 输入输出样例 #1
### 输入 #1
```
2 3 3 3
0 20
6 6 6
1 1
2 2
1 2
```
### 输出 #1
```
0
1
1
```
## 输入输出样例 #2
### 输入 #2
```
6 3 3 3
6 5 10 15 19 7
2 5 10
1 6
1 4
4 6
```
### 输出 #2
```
3
3
2
```
## 说明/提示
#### 样例解释:
**#样例1** : $20$ 经过一次 $op$ 操作(除以 $3$ 向下取整)可以变成 $6$,而 $0$ 不能经过若干次 $op$ 操作变成 $6$ 。
所以区间 $[1,1]$ 最多消灭 $0$ 个数,消灭最多数前提下最少需要 $0$ 个 "原数",区间 $[1,2],[2,2]$ 最多消灭 $1$ 个数,消灭最多数前提下最少需要 $1$ 个 "原数" 。
**#样例2** : $2$ 能消灭 $\{6,19,7\}$ , $5$ 能消灭 $\{5,15\}$ , $10$ 能消灭 $\{10\}$ , 所以区间 $[1,6],[1,4]$ 最少能用所有 "原数" 全部消灭,区间 $[4,6]$ 能用 $2,5$ 全部消灭。
#### 数据范围:
对于 $30\%$ 的数据:$n\le100,m\leq10, d=2, q\le 10$
对于 $100\%$ 的数据:$n\le5\times 10^{5},m\leq60,2\leq d\leq10,q\le10^{6},0\le a_i,b_i\le 2^{63}$
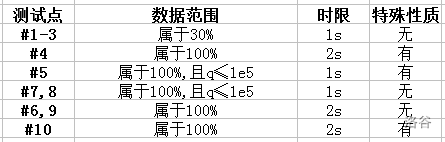
特殊性质:数据经过构造。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=1e6;
struct node{
ll l,r,sum;
}tr[4*N+5];
struct xd{
ll l,r,f;
}b[N+5];
ll n,m,d,q;
ll a[N+5],ans[N+5];
ll pre[N+5],lst[N+5];
ll ys[N+5],dy[N+5];
map<ll,bool> mp;
void updata(ll p){
tr[p].l=tr[2*p].l;
tr[p].r=tr[2*p+1].r;
tr[p].sum=tr[2*p].sum+tr[2*p+1].sum;
return;
}
void build(ll p,ll l,ll r){
if(l==r){
tr[p].l=l;
tr[p].r=r;
return;
}
ll mid=(l+r)>>1;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
updata(p);
return;
}
void change(ll p,ll x,ll y){
if(tr[p].l==x && tr[p].r==x){
tr[p].sum+=y;
return;
}
if(x<=tr[2*p].r) change(2*p,x,y);
else change(2*p+1,x,y);
updata(p);
return;
}
ll searchh(ll p,ll l,ll r){
if(r<l) return 0;
ll s=0;
if(tr[p].l==l && tr[p].r==r) return tr[p].sum;
if(tr[2*p].r>=r) s+=searchh(2*p,l,r);
else if(tr[2*p+1].l<=l) s+=searchh(2*p+1,l,r);
else{
s+=searchh(2*p,l,tr[2*p].r);
s+=searchh(2*p+1,tr[2*p+1].l,r);
}
return s;
}
bool cmp(xd l1,xd l2){
return l1.r<l2.r;
}
int main(){
memset(dy,-1,sizeof(dy));
scanf("%lld%lld%lld%lld",&n,&m,&d,&q);
for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
for(ll i=1;i<=m;i++) scanf("%lld",&ys[i]),mp[ys[i]]=1;
for(ll i=1;i<=n;i++){
ll num=a[i],w=-1;
if(mp[num]) w=num;
while(num){
num/=d;
if(mp[num]) w=num;
}
dy[i]=w;
}
// for(ll i=1;i<=n;i++) cout<<dy[i]<<" ";
// return 0;
for(ll i=1;i<=q;i++){
scanf("%lld%lld",&b[i].l,&b[i].r);
b[i].f=i;
// cout<<i<<endl;
}
for(ll i=1;i<=n;i++){
if(dy[i]==-1) continue;
pre[i]=lst[dy[i]];
lst[dy[i]]=i;
}
build(1,1,n);
sort(b+1,b+1+q,cmp);
ll nxt=1;
for(ll i=1;i<=q;i++){
while(nxt<=b[i].r){
if(dy[nxt]==-1){
nxt++;
continue;
}
if(pre[nxt]) change(1,pre[nxt],-1);
change(1,nxt,1);
nxt++;
}
ans[b[i].f]=searchh(1,1,b[i].r)-searchh(1,1,b[i].l-1);
}
for(ll i=1;i<=q;i++) printf("%lld\n",ans[i]);
return 0;
} 时间限制3s,评测结果RE+TLE,找错误,并在不改变代码原本写法的情况下修正







 本文介绍了一种利用差分技巧优化树状数组的方法,并通过一个具体的编程实例展示了如何使用差分树状数组来高效地解决区间更新问题。文章包含了完整的代码实现及解析。
本文介绍了一种利用差分技巧优化树状数组的方法,并通过一个具体的编程实例展示了如何使用差分树状数组来高效地解决区间更新问题。文章包含了完整的代码实现及解析。
















 422
422

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








