勾股定理 —— 证明大全

更多精彩的证明方式请见英文维基 Pythagorean theorem

a2+b2=c2

2002 年北京召开的世界数学大会，会徽如下：

c2=4⋅12ab+(b−a)2⇒c2=a2+b2

1. 不同分割方法

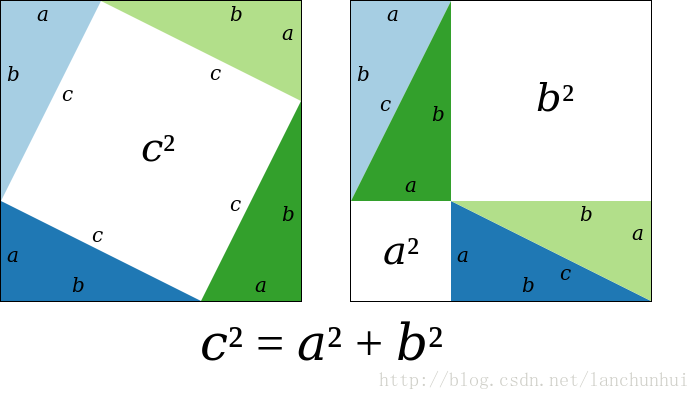
构造两个边长为 a+b 的正方形，则采用不同的分割方法，便会有，左边白色区域的面积等于右边白色区域的面积：

c2=a2+b2

转载于:https://www.cnblogs.com/mtcnn/p/9421738.html