（笔试题）和一半的组合数

题目：

若对于整数N，在集合｛1，2……，N｝中找出m个数，使其和等于剩下的N-m个数的和。返回所有可能的组合数，N<10000（不能使用任何库函数）。

思路：

组合问题都可以通过回溯法+剪枝来解决

根据题目的意思，其实就是将1-N分为和相等的两半，其满足的前提条件是1-N的总和为偶数（只有偶数才能分成相等的两份）。

在满足总和为偶数的情况下，就通过回溯法来求组合的可能性，适当的剪枝可以减小复杂度。

代码：

#include<iostream>
#include<vector>

using namespace std;

#define N 8
int count=0;

void Sum(int *nums,vector<int> out,int sum,int total,int n,int idx){
		if(idx>n || (sum*2)>total)
			return;
		if(sum*2==total){
			for(vector<int>::iterator it=out.begin();it!=out.end();it++)
				cout<<*it<<" ";
			cout<<endl;
			count++;
			return;
		}

		out.push_back(nums[idx]);
		Sum(nums,out,sum+nums[idx],total,n,idx+1);
		out.pop_back();
		Sum(nums,out,sum,total,n,idx+1);
}

int main(){
	int a[N];
	for(int i=0;i<N;i++){
		a[i]=i+1;
	}
	vector<int> out;
	int total=(1+N)*N/2;

	if(total%2==0){
		Sum(a,out,0,total,N,0);
		cout<<"Total Count is "<<count<<endl;
	}
	else
		cout<<"Not Found"<<endl;
	return 0;
}

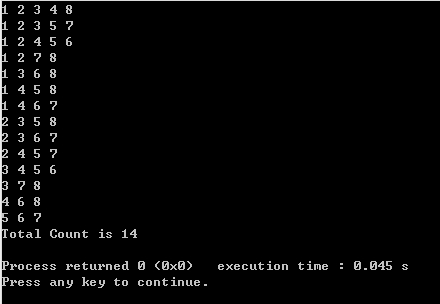
运行结果：

转载于:https://www.cnblogs.com/AndyJee/p/4528122.html