本文深入解析LCA（最近公共祖先）算法，涵盖信息学竞赛中常见的两种求解方法：倍增算法与Tarjan算法。详细介绍了算法原理、实现步骤及代码示例，适合初学者快速掌握。
什么是LCA?
话不多说,同志们先来康康LCA是什么东西.(逃
LCA“光辉”是印度斯坦航空公司(HAL)为满足印度空军需要研制的单座单发轻型全天候超音速战斗攻击机，主要任务是争夺制空权、近距支援，是印度自行研制的第一种高性能战斗机。------摘自百度百科
当然,同志们认识的LCA可不是那个研制了三十年的烂玩意.
在信息学竞赛中,LCA指的是"Lowest Common Ancestors",即"最近公共祖先".算法目的是在一颗有根树中,求出结点\(x\)和\(y\)最近的公共祖先.
那么什么是最近的公共祖先呢?斯大林格勒的拖拉机工人们给出了这样一幅图:
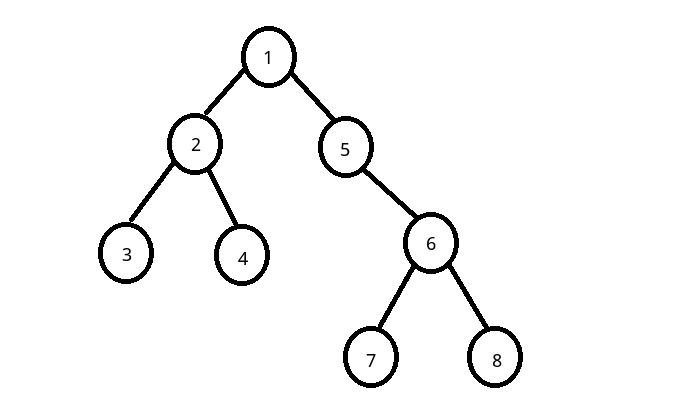
首先我们得理解祖先的概念.对与任意一个树上的结点,与它有亲缘关系,且深度比它小的结点都是它的祖先.
在这幅图中,3号结点的祖先为2和1,6号结点的祖先为5和1,所以它们有公共的祖先1,所以说3和6的LCA为1.
再举一个例子,3结点的祖先为2和1,4号结点的祖先为2和1,它们有公共祖先2和1,但是2是距离它们最近的祖先,所以说3和4的LCA为2.
怎样建设求出LCA?
求LCA一般可用到倍增,Tarjan(不是用于缩点那个Tarjan)这两种算法,在这里一一讲解.
倍增版LCA
主体思想(请勿联想到某金姓领导人)
倍增是一种二进制拆分的思想,其已广泛应用于ST表,求解LCA等算法,为我国生产力的发展,推进共产主义的早日实现做出了巨大贡献.
实现方式
类比ST表的实现方式,同志们可以设\(path[i][j]\)为结点i向上跳\(2^j\)后到达的结点.显然,\(path[i][0]\)就是\(i\)结点的父亲.
那么如何进行二进制拆分呢?显然,\(path[i][j-1]\)向上再跳\(2^{j-1}\)次后到达的结点就是\(path[i][j]\).
于是同志们可以这样预处理:
path[i][j]=path[f[i][j-1]][j-1];意为:\(i\)号结点向上跳\(2^j\)个长度到达的结点,等于\(i\)号结点向上跳\(2^{j-1}\)个结点到达的结点再向上跳\(2^{j-1}\)个结点.
然后将两个结点提至同一深度,不断地向上跳即可求出它们的LCA.
建设求出LCA的具体步骤
进行预处理.
把结点x和y调整至同一高度.
将结点x和y同时向上调整,保持深度一致且二点不相会.具体地说,就是将\(x\)和\(y\)以此向上走\(k\)=\(2^{logn}\),...,\(2^1\),\(2^0\)步,如果\(path[x][k]\)!=\(path[y][k]\)(即两点还未相会),就令\(x\)=\(path[x][k]\),\(y\)=\(path[y][k]\).
这时\(x\)与\(y\)只差一步就相会了,返回\(path[x][0]\),即\(x\)的父亲,即为\(x\)和\(y\)的LCA.
该算法的时间复杂度为\(O(log2(Depth))\)
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iomanip>
#include<vector>
using namespace std;
struct edge
{
int next,to;
}e[1000010];
int n,m,s,size;
int head[500010],depth[500010],path[500010][51];
void EdgeAdd(int,int);
int LCA(int,int);
void DFS(int,int);
int main()
{
memset(head,-1,sizeof(head));
scanf("%d%d%d",&n,&m,&s);
for(int _=1;_<=n-1;_++)
{
int father,son;
scanf("%d%d",&father,&son);
EdgeAdd(father,son);
EdgeAdd(son,father);
}
DFS(s,0);
for(int _=1;_<=m;_++)
{
int a,b;
scanf("%d%d",&a,&b);
printf("%d\n",LCA(a,b));
}
return 0;
}
void EdgeAdd(int from,int to)
{
e[++size].to=to;
e[size].next=head[from];
head[from]=size;
}
void DFS(int from,int father)
{
depth[from]=depth[father]+1;
path[from][0]=father;
for(int _=1;(1<<_)<=depth[from];_++)
{
path[from][_]=path[path[from][_-1]][_-1];
}
for(int _=head[from];_!=-1;_=e[_].next)
{
int to=e[_].to;
if(to!=father)
{
DFS(to,from);
}
}
}
int LCA(int a,int b)
{
if(depth[a]>depth[b])
{
swap(a,b);
}
for(int _=20;_>=0;_--)
{
if(depth[a]<=depth[b]-(1<<_))
{
b=path[b][_];
}
}
if(a==b)
{
return a;
}
for(int _=20;_>=0;_--)
{
if(path[a][_]==path[b][_])
{
continue;
}
else
{
a=path[a][_];
b=path[b][_];
}
}
return path[a][0];
}
Tarjan版LCA
Tarjan版的LCA是离线的,而上文介绍的倍增版LCA是在线的,所以说如果不是直接输出LCA的话,需要一个数组来记录它.
主体思想
从根结点遍历这棵树,遍历到每个结点并使用并查集记录父子关系.
实现方式
用并查集记录父子关系,将遍历过的点合并为一颗树.
若两个结点\(x\),\(y\)分别位于结点\(a\)的左右子树中,那么结点\(a\)就为\(x\)与\(y\)的LCA.
考虑到该结点本身就是自己的LCA的情况,做出如下修改:
若\(a\)是\(x\)和\(y\)的祖先之一,且\(x\)和\(y\)分别在\(a\)的左右子树中,那么\(a\)便是\(x\)和\(y\)的LCA.
这个定理便是Tarjan版LCA的实现基础.
具体步骤
当遍历到一个结点\(x\)时,有以下步骤:
把这个结点标记为已访问.
遍历这个结点的子结点\(y\),并在回溯时用并查集合并\(x\)和\(y\).
遍历与当前结点有查询关系的结点\(z\),如果\(z\)已被访问,则它们的LCA就为\(find(z)\).
需要同志们注意的是,存查询关系的时候是要双向存储的.
该算法的时间复杂度为\(O(n+m)\)
Tarjan版的LCA很少用到,但为了方便理解,这里引用了参考文献2里的代码,望原博主不要介意.
代码:
#include<bits/stdc++.h>
using namespace std;
int n,k,q,v[100000];
map<pair<int,int>,int> ans;//存答案
int t[100000][10],top[100000];//存储查询关系
struct node{
int l,r;
};
node s[100000];
/*并查集*/
int fa[100000];
void reset(){
for (int i=1;i<=n;i++){
fa[i]=i;
}
}
int getfa(int x){
return fa[x]==x?x:getfa(fa[x]);
}
void marge(int x,int y){
fa[getfa(y)]=getfa(x);
}
/*------*/
void tarjan(int x){
v[x]=1;//标记已访问
node p=s[x];//获取当前结点结构体
if (p.l!=-1){
tarjan(p.l);
marge(x,p.l);
}
if (p.r!=-1){
tarjan(p.r);
marge(x,p.r);
}//分别对l和r结点进行操作
for (int i=1;i<=top[x];i++){
if (v[t[x][i]]){
cout<<getfa(t[x][i])<<endl;
}//输出
}
}
int main(){
cin>>n>>q;
for (int i=1;i<=n;i++){
cin>>s[i].l>>s[i].r;
}
for (int i=1;i<=q;i++){
int a,b;
cin>>a>>b;
t[a][++top[a]]=b;//存储查询关系
t[b][++top[b]]=a;
}
reset();//初始化并查集
tarjan(1);//tarjan 求 LCA
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
