Python实现——一元线性回归(最小二乘法)

最新推荐文章于 2024-06-16 19:46:23 发布

weixin_30729609

最新推荐文章于 2024-06-16 19:46:23 发布

阅读量724

点赞数 1

CC 4.0 BY-SA版权

文章标签：数据结构与算法 python 开发工具

原文链接：http://www.cnblogs.com/LOSKI/p/10639611.html

本文介绍了如何使用最小二乘法进行线性回归分析，并通过Python编程实现了线性回归模型。文中详细解释了最小二乘法的基本原理，包括偏差最小化的数学背景及其在实际数据集上的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2019/3/24
线性回归——最小二乘法公式法
暂时用python成功做出来了图像，但是其中涉及到的公式还是更多的来自于网络，尤其是最小二乘法公式中的两个系数的求解，不过目前看了下书高数也会马上提及（虽然可能不会讲这两个公式），但是运用的知识其实还是目前能够接受的：偏导，二元方程。乍一看其实也没什么，只是由于有了求和符号的干扰让计算显得复杂。
最小二乘法-公式推导
该博客中对其的推导看起来比较简洁容易接受，其中结尾公式的计算不难让人想到线性代数中的向量乘积运算，但是那样的表示方法我并不熟练，等到系统的学习线代后再深挖....吧。
总的来说：y=a+bx 便是我们的预测函数。然而不同于以往的是变量变为了a与b两个系数，从这里也不难看到其实若是二次拟合也有一个好处那便是虽然x中含有二次项而系数中并没有，仍然是一次方程。
而我们所要做到的便是能够让这个函数在基于现有数据的参照下偏差最小，而偏差值的衡量我们将会用方差来表示，不选择简单的做差是由于做差势必会带来正负的区别，而由此又会导致偏差之间相互抵消，而若是加上绝对值的话又要涉及判断，因此方差成为了简单直接的方式。
之后的求解，简单来说就是分别对两个系数进行求偏导，在之后，我们再转换一下观念。

虽然我们目前来看是把系数当作了未知数，但是实际上这还是关于x，y的方程，对于x，y的方差，应视其为二次函数，也因此最小值的求解应该在导数0点取得。
（有待商榷，这只是我目前的理解）

因此再分别对应回两个偏导为零继续求解，其中关于a的方程较为简单，而b则会麻烦一点。

而在我的python实现中
前两个库函数可能没有使用到
修正：上两个函数应该为excel导入的函数，之前应该是忘了

import xlrd
import xlwt
import matplotlib.pyplot as plt
import numpy as np

此处则对应的是读取数据

workbook=xlrd.open_workbook(r'1.xls')
sheet=workbook.sheet_by_index(0)
cols1=sheet.col_values(0)   #获取第一列
cols2=sheet.col_values(1)   #获取第二列

以下则是在为最后一步的公式提供准备每个参量，把单个值提前表示出来

s1=0
s2=0
s3=0
s4=0

for i in range(n):
    s1 = s1 + cols1[i]*cols2[i]
    s2 = s2 + cols1[i]
    s3 = s3 + cols2[i]
    s4 = s4 + cols1[i]*cols1[i]

最后这里就是公式的求解，相信就算没看前面推导，也能大概懂点其中每个量的相互关系以及上面所准备的参量的意义

b = (s2*s3-n*s1)/(s2*s2-s4*n)
a = (s3 - b*s2)/n

最后便是作图，plt.scatter()绘制散点图，plt.plot是折线图，而np.linspace()则需要根据实际数据的情况进行合理取值

plt.scatter(cols1,cols2,color = 'blue') 
x=np.linspace(0,100,1000)
y=b*x+a
plt.plot(x,y,color="red")
plt.show()

这个是我第一次成功运行后得出的图像（实验室提供的第一组数据）虽然可能更适合二次拟合？但是大概也是我的第一次成功尝试吧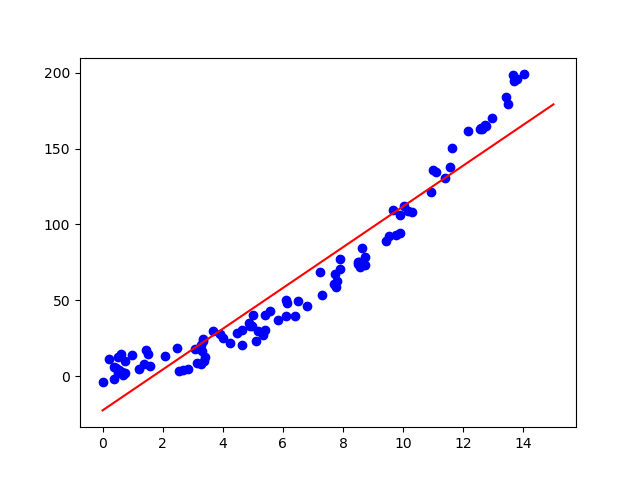
Figure_1

整体代码如下

import xlrd
import xlwt
import matplotlib.pyplot as plt
import numpy as np
workbook=xlrd.open_workbook(r'2.xls')

sheet=workbook.sheet_by_index(0)
cols1=sheet.col_values(0)   #获取第一列
cols2=sheet.col_values(1)   #获取第二列

#plt.plot(cols1,cols2)


n=100
s1=0
s2=0
s3=0
s4=0


for i in range(n):
    s1 = s1 + cols1[i]*cols2[i]
    s2 = s2 + cols1[i]
    s3 = s3 + cols2[i]
    s4 = s4 + cols1[i]*cols1[i]

b = (s2*s3-n*s1)/(s2*s2-s4*n)    #最小二乘法获取系数的公式
a = (s3 - b*s2)/n    #最小二乘法获取系数的公式
plt.scatter(cols1,cols2,color = 'blue') 
x=np.linspace(0,15,100)
y=b*x+a
plt.plot(x,y,color="red")
plt.show()

PS:谨记，利用excel导入数据的时候一定要记得检查表格中数据的类型，由于当时一开始表格内部的数并不是以数字存储的，读入的时候可能是以字符？文本？反正是不能正确显示，直接就是一个莫名其妙的y=x图像，惊了我都，一直以为是我代码错误，后来才觉察到。
我还特地又搞了一回错的来纪念这个奇怪的情况...
Figure_1
来自蒟蒻的瑟瑟发抖...【对萌新的我造成了极大的伤害/蒙圈