COGS 2581 无聊的会议V2

传送

题目大意

给定一个长为\(n\)的序列,定义\(y\)在三元对\((x,y,z)\)中成为中心轴当且仅当同时满足:\(a_x = a_y = a_z,y-x=z-y,x<y<z\)对于每个位置\(i\)求使\(i\)成为中心轴的三元对的数量.

题解

首先我们发现\((a_i \leq 5)\)所以我们可以分别枚举0~5这6个数字
假设当前枚举到\(num\)，那么把等于\(num\)的置为1,其余的置为0
那么现在问题转化成了怎么求出值全为1的三元对
观察下图:假设方框所选作为中心轴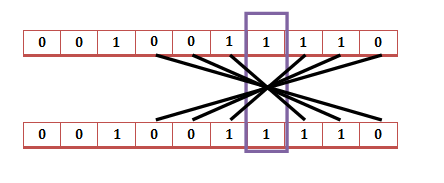

则中心轴的数量+1当且仅当黑线的两端均为1
我们发现若黑线表示两数相乘,那么乘法运算恰好符合上一句
并且我们发现这构成了卷积的形式
所以我们使用FFT加速
由数学知识可以得到,以i为中心轴的三元对个数储存于\(2i\)中
但是因为我们计算时没有保证\(x < z\)所以不要忘了\(ans/=2\)

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
    x=0;char ch;bool flag = false;
    while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
    while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
const int maxn = 1048576+1+11424;
const int mod = 23068673;
const int pri_rt = 3;
int e[maxn],ie[maxn],len;
inline int qpow(int x,int p){
    int ret = 1;
    for(;p;x=1LL*x*x%mod,p>>=1) if(p&1) ret=1LL*ret*x%mod;
    return ret;
}
inline void init(int n){
    len = n;
    int bas = qpow(pri_rt,(mod-1)/len);
    int inv = qpow(bas,mod - 2);
    e[0] = ie[0] = 1;
    for(int i=1;i<n;++i){
        e[i] = 1LL*e[i-1]*bas%mod;
        ie[i] = 1LL*ie[i-1]*inv%mod;
    }
}
inline void FNT(int n,int *x,int *w){
    for(int i=0,t=0;i<n;++i){
        if(i > t) swap(x[i],x[t]);
        for(int j=n>>1;(t^=j) < j;j>>=1);
    }
    for(int m=2;m<=n;m<<=1){
        int k = m>>1,t = len/m;
        for(int i=0;i<n;i+=m){
            for(int j=0,p=0;j<k;++j,p+=t){
                int u = 1LL*x[i+j+k]*w[p]%mod;
                x[i+j+k] = x[i+j] - u;
                if(x[i+j+k] < 0) x[i+j+k] += mod;
                x[i+j] += u;
                if(x[i+j] >= mod) x[i+j] -= mod;
            }
        }
    }
    if(w == ie){
        int inv = qpow(n,mod-2);
        for(int i=0;i<n;++i) x[i] = 1LL*x[i]*inv%mod;
    }
}
int a[maxn],c[maxn],ans[maxn];
int main(){
    freopen("OXO.in","r",stdin);
    freopen("OXO.out","w",stdout);
    int n;read(n);
    for(int i=0;i<n;++i) read(a[i]);
    int len;for(int i=1;(i>>2)<n;i<<=1) len = i;
    init(len);
    for(int num=0;num<=5;++num){
        memset(c,0,sizeof c);
        for(int i=0;i<n;++i) if(a[i] == num) c[i] = 1;
        FNT(len,c,e);
        for(int i=0;i<len;++i) c[i] = 1LL*c[i]*c[i]%mod;
        FNT(len,c,ie);
        for(int i=0;i<len;++i){
            if( (i&1) || a[i>>1] != num ) continue;
            if(c[i] < 0) c[i] += mod;
            ans[i>>1] += c[i]>>1;
        }
    }
    for(int i=0;i<n;++i) printf("%d\n",ans[i]);
    getchar();getchar();
    return 0;
}

转载于:https://www.cnblogs.com/Skyminer/p/6396128.html