Pollard Rho算法浅谈

最新推荐文章于 2025-04-04 13:59:04 发布
最新推荐文章于 2025-04-04 13:59:04 发布
阅读量1k 收藏 17
点赞数 2
CC 4.0 BY-SA版权
文章标签： 数据结构与算法
原文链接：http://www.cnblogs.com/Iamafool/p/10924390.html
本文介绍Pollard Rho算法，它是一种用于大整数因数分解的算法，具有空间复杂度Θ(1)的优势。文中阐述了其原理，涉及生日悖论、Miller Rabin素性测试等，还介绍了算法的做法及多种优化方法，如GCD优化、过河拆桥优化法等，并给出P4718的代码。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

Pollard Rho介绍

Pollard Rho算法是Pollard[1]在1975年[2]发明的一种将大整数因数分解的算法

其中Pollard来源于发明者Pollard的姓，Rho则来自内部伪随机算法固有的循环

Pollard Rho算法在其他因数分解算法[3]中不算太出众，但其空间复杂度Θ(1)的优势和好打的代码使得OIer更倾向于使用Pollard Rho算法

毕竟试除法太慢了，谁没事打Pollard Rho不打试除法

 

Pollard Rho原理

生日悖论

如果一年只有365天（不计算闰年），且每个人的生日是任意一天的概率均相等，那么只要随机选取23人，就有50%以上的概率有两人同一天生日

解释：第一个人不会和前面的人重生日（因为前面没有人），第二个人不重生日的概率为364/365，第三个人363/365……以此类推，那么只要到第23个人，就有，说明这时就有50%以上的概率有两人同生日

更多的，当一年有n天时，只要人数到达Θ(sqrt(n))的数量级，有至少两个人同一天生日的概率就可以达到50%以上

图象表达：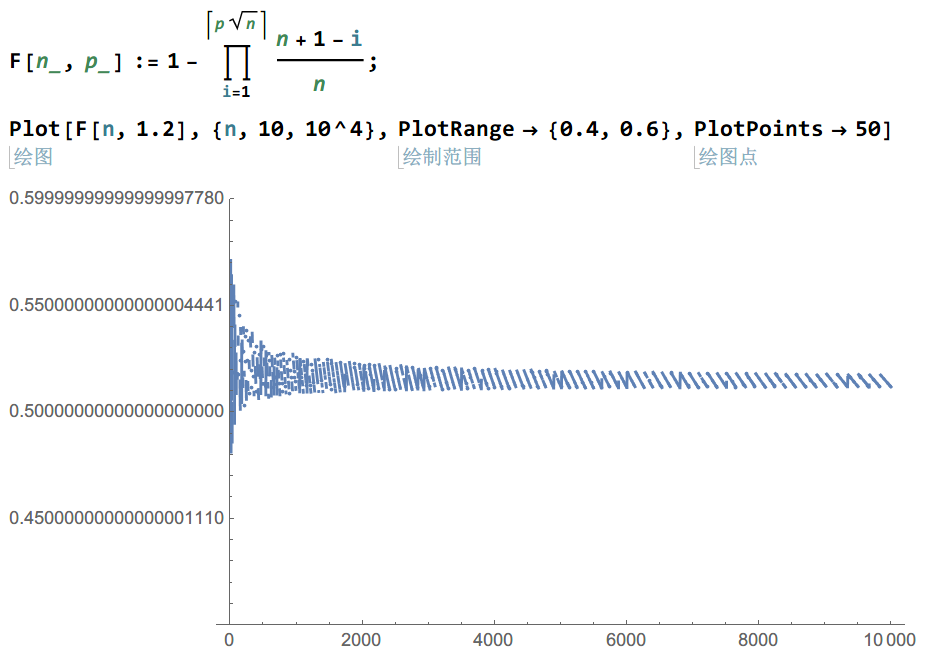

Miller Rabin素性测试[4][4']

其实Miller Rabin素性测试不是那么重要（因为不是Pollard Rho算法的核心），但没有它，Pollard Rho算法会被试除法拖慢到比朴素算法更差

这里就不再赘述，想要学习的请移步至维基百科（百度百科真是垃圾）

快速幂&比硬件还慢的快速乘&GCD

这应该是大多数数论算法的标配，不会的请先百度或谷歌

Floyd判圈算法[5]

Floyd判圈算法又叫龟兔赛跑算法，是用差速转移的方式快速判断是否进入环的算法

想象有一只兔子和一只乌龟按一个确定函数从同一个起点移动，兔子每次可以转移两次，乌龟可以转移一次

（OI算法中一张奇怪的图片）

那么如果这个确定函数上没有环，那么兔子一定会在乌龟前面，二者一定不会相交

否则，由于函数上有环，兔子一定会“追上”乌龟，也就是“套圈”

不仅如此，对算法分析可知，当兔子“追上”乌龟时，兔子也一定跑了刚好一圈（就是不证明，你来打我呀）

 

Pollard Rho算法的做法

介绍所有算法前先要声明一下：在每次操作前要先判断是不是素数，否则找不出原数的非平凡因子

这里要用Miller Rabin素性测试快速判断，以保证其高效性（不然提到这家伙是干什么的）

GCD优化+随机化试除法

试除法是一种朴素的因数分解算法，加了随机化后其实并没有多大用而且还更慢了

但是如果我们退而求其次——不直接寻找因子，而是寻找因子的倍数，然后用GCD找到因子本身呢

随机寻找到一个因子的倍数的概率为，确实比直接找因子的随机化试除法好了一点点，但当因子很大时依旧没什么用

PS：在Pollard Rho算法中随机数算法一般用F(x)=x2+c（这个函数具有混沌性，实现又简单，所以比较常用，我也不知道能不能用其他函数，应该是可以的）

向成熟的Pollard Rho算法迈进

把原来的一个随机数变成两个数的差，这样就得到了比较常见的Pollard Rho算法模板

看上去似乎并没有什么用（实际上对效率也没什么帮助），但是我们可以把两个随机数设为Floyd判圈算法中的“兔子”和“乌龟”，从而在走上“不归路”前及时退出

PS：看上去似乎到现在都还没有用到生日悖论的概率增大，但是实际上当寻找次数比较小时不记录的随机和记录的随机概率相近

减少GCD数目——过河拆桥优化法

每次产生一对随机数都要求一次GCD，对算法的效率有着很大影响。有什么办法可以减少求GCD的次数呢？

我们可以发现，把多个数相乘再取GCD一定不会使找出的因子大小更小

所以说，我们可以将K个差相乘，然后GCD一次判断，找到非平凡因子的概率就更大了

需要注意的是，当乘积变成要求分解的数的倍数时，说明最后一对随机数一定对结果有贡献，数对差一定是一个因子的倍数

不仅如此，当循环因为找到环而退出时应该把已有的乘积进行判断（连尸体都不放过）

PS：这里的K一般取127，我也不知道为什么

《算法导论》的优化——倍增求圈法

当随机数的转移算法比较复杂时，Floyd判圈算法的多次转移就会成为性能的瓶颈。有什么办法可以少转移呢？

可以想到，我们可以不直接寻找环的出现，而是在转移时标记一个记录点，当发现走到了记录点，就说明我们已经走了至少一圈环

但又要怎么打标记点呢？打得太少会退化，打得太多又会影响效率，必须要和环的长度差不多才行，这就变成了猜测环的长度的问题了

而每次猜测环的长度可以用倍增的方法，首先猜环的长度在K以内，如果没走到，那么不是猜小了就是记录点选错了，把记录点换成现在这个点，再继续猜测环的长度为2K

所以又怎么替代Floyd判圈算法呢？由于记录点自身也是随机数，具有一定的随机性，那就干脆直接代替Floyd判圈算法的“乌龟”得了

在已有算法上卡一卡常——让子弹再飞一会

  • Miller Rabin素性测试的正确性很高，按洛谷P4718的题解中_皎月半洒花在测试时只要测2和61就能过，但正确性也许无法保证，需要2,3,5,7,11,13,17,19和23都测一遍[6]
  • 用register运算符修饰临时变量，优化硬件速度（register可以让数据被存储到更快的CPU寄存器中）
  • 用快一点的快速乘算法，并尽量减少强制类型转换的次数

 

P4718的代码——Pollard Rho算法

 1 #define LL long long
 2 bool IsPrime(LL);//返回素性测试结果
 3 LL GCD(LL,LL);//返回两个数的GCD
 4 LL Mix(LL,LL,LL);//返回两个数在模运算下的乘积
 5 
 6 void MaxFactor(LL n,LL &ans){
 7         if(n==1||n<=ans||IsPrime(n)){
 8         ans=max(ans,n);
 9         return;//判断特殊情况：n为1或素数，n一定不能更新ans
10     }
11     for(LL c=rand()%(n-1)+1;;c++){
12         //为防止随机数无效化，使用死循环
13         LL t1=rand()%(n-1)+1,t2=(Mix(t1,t1,n)+c)%n;
14         LL p=1,i=0,g=0;
15         while(t1!=t2){
16             p=Mix(p,abs(t1-t2),n);
17             if(!p){//乘积为0时说明找到了一个因子
18                 g=GCD(n,abs(t1-t2));
19                 if(g>1&&g<n){
20                     MaxFactor(g,ans);
21                     MaxFactor(n/g,ans);
22                 }
23                                 return;
24             }
25             ++i;
26             if(i==127){//当有127个数时强制测试
27                 g=GCD(n,p);
28                 if(g>1&&g<n){
29                     MaxFactor(g,ans);
30                     MaxFactor(n/g,ans);
31                     return;
32                 }
33                 p=1,i=0;
34             }
35             t1=(Mix(t1,t1,n)+c)%n;
36             t2=(Mix(t2,t2,n)+c)%n;
37             t2=(Mix(t2,t2,n)+c)%n;
38         }
39         g=GCD(n,p);
40         if(g>1&&g<n){//循环退出后收尾
41             MaxFactor(g,ans);
42             MaxFactor(n/g,ans);
43             return;
44         }
45     }
46 }

 

参考资料

洛谷日报：https://www.luogu.org/blog/zenyz/pollardrho-kuai-su-fen-xie-zhi-yin-shuo

P4718题解：https://www.luogu.org/problemnew/solution/P4718

Pollard Rho算法——维基百科：https://en.wikipedia.org/wiki/Pollard%27s_rho_algorithm

Miller Rabin素性测试——维基百科：https://zh.wikipedia.org/wiki/%E7%B1%B3%E5%8B%92-%E6%8B%89%E5%AE%BE%E6%A3%80%E9%AA%8C

——会某人

转载于:https://www.cnblogs.com/Iamafool/p/10924390.html

Python pollard rho大数分解算法详解及源码
希望我的博客，能帮上你解决学习中工作中所遇到的问题
08-13 833
pollard rho大数分解算法是一种用于分解大整数的算法。它基于Floyd循环检测算法，通过随机生成一个序列，再利用序列的循环来找到大整数的因子。 算法步骤如下： 随机选择一个整数x作为起始点。 定义两个函数f(x)和g(x)，分别通过特定的函数关系将x映射到下一个数。 重复执行以下步骤直到找到因子或者无法找到因子为止： 计算f(x)和f(f(x))，分别得到x1和x2。 计算g(x)和g(g(x))，分别得到y1和y2。 使用欧几里得算法计算x2和x1之间的最大公因数d。 若d为大整数n，则找到
Python:实现pollard rho大数分解算法(附完整源码)
希望我的博客，能帮上你解决学习中工作中所遇到的问题
08-01 1264
Python:实现pollard rho大数分解算法(附完整源码)
Pollard Rho算法
dashengchong6303的博客
08-28 1781
原理 Pollard Rho算法是一个非常玄学的算法(我个人还不是很懂其原理),作用是分解出一个数的非平凡因子(除1和它本身),通常作用于对大数的质因数分解.期望复杂度为O(n1/4).总体来说运行效果还是相当不错的. 算法核心:y=x,x=x*x+c.其中x,y初值是随机生成的,c也是随机生成的常数,假设算法求的是n的因子,最后要判断的是g=gcd(abs(y-x),n),如果g大...
Pollard_rho算法
仰望蓝天的博客
06-19 437
思路代码 int find_factorplus(int N) { a = 2; for（ int i= 1; i &lt;= 1000000; i++ ) { b = f(a); p = GCD( abs( b - a ) , N); if( p &gt; 1 ) return p;//Found factor: p ...
【学习笔记】Pollard-Rho算法
七代目鸽影
03-12 1702
代码能力 ≈ 0
Pollard-rho算法[因子分解算法]
weixin_30861797的博客
02-11 357
试除法:最简单的因数分解算法，从$ 2 $到$ \sqrt n $一个一个试。 试除法(改进):从$ 2 $到$ \sqrt n $挑素数一个一个试。 然而这样复杂度是相当高的。 生日悖论：指如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。 我们在$ [2,n) $取一个数，该数是$ n $的因子的概率很小. 我们取$ k $ 个数$ x_1,x_2...
Pollard Rho算法思想
07-28
Pollard Rho 算法思想 Pollard Rho 算法思想是由 John M. Pollard 在 1975 年提出的第二种因数分解方法。该方法基于以下几点： 1. 假定有两个整数 x 和 y，使得 p 可以整除 xy，但是 n 不能整除 xy。 2. 可以证明 ...
使用Pollard_rho算法分解质因数
qq_44463933的博客
04-01 784
Pollard_rho算法是找到一个数的最大质因数，我参考此算法进行修改，实现了将一个数分解为质因数相乘形式的程序。
Pollard-Rho算法
到处遛鸟刑警
08-16 318
用途：分解大数因数 复杂度 : O(很快) 基本思路: 考虑构造一个序列x1,x2,x3....xnx1,x2,x3....xnx1,x2,x3....xn 如果有$d = gcd(abs(xi , xi + 1) , N) > 1 $ 等价于 d是N的一个因数 但，构造序列的方法有很多，该算法选用了一种好写 + 好想的 ： （伪随机方法构造序列） 令Xi=(Xi−1∗Xi−1+C) 令Xi = (Xi - 1 * Xi - 1 + C) % N 令Xi=(Xi−1∗Xi−1+C) 然后该算法的基础
Pollard-Rho算法详解
09-12
Pollard-Rho算法详解
【模板】Pollard-Rho算法
Brute♂force
01-21 390
题目 https://www.luogu.com.cn/problem/P4718 思路 真的是阴间卡常模板题 blog 代码 #include<bits/stdc++.h> #define ll long long #define ld long double #define ull unsigned long long using namespace std; int T; ll ans,n; inline ll mul(ll x,ll y,ll p) { ll yjy=(ld)x/p*y
Pollard_Rho
YT910811的博客
03-16 449
目录 题面 前置知识: 1.Miller_Rabin (1)费马小定理 (2)二次探测 2.快速幂,快速乘 3.gcd 做法 方法一:试除法 方法二:ran...
分解因子算法——Pollard rho算法
国科大网安二班的博客
03-22 3599
分解因子算法——Pollard ρ\rhoρ 算法 攻击RSA密码体制最明显的方法就是分解大整数。关于大整数分解的算法有许多，常见的有试除法、p±1p\pm1p±1算法、Pollard ρ\rhoρ算法、数域筛法、二次筛法等等。这篇分享的就是其中之一的Pollard ρ\rhoρ算法。 我们说因子分解，很多时候并不一定要把大整数nnn彻底分解成素数乘积，而是求出nnn的某个非平凡因子即可。求大整数的一个因子固然困难，但是Euclidean算法告诉我们求两个数的最大公因子是可以在O(log⁡n)O(\log
大整数分解——Pollard Rho算法
xffyjq的博客
09-28 9754
延续上一篇，这次来讲一讲大整数分解算法的应用。要解决的问题很简单，对一个整数进行分解质因数。首先还是效率非常低的暴力算法，相信大家都会，不多提。和上次一样，当数达到非常大的时候，分解将变得非常困难。于是这次又带来一个提升分解速度的“非完美”算法。之所以打引号，是因为这次不完美的不是结果，而是时间效率。Pollard Rho算法分解一个数n的过程大体上是这样子的：1、找到一个数p，使得p|np|n，将
Pollard rho算法总结
Harris-H的博客
07-06 816
Pollard rho算法总结 前置知识 快速幂 快速乘 Miller Rrabin判断素数O(klog3n)O(klog^3n)O(klog3n) 快速幂 太简单了，不讲 ll ksm(ll a,ll n,ll p){ ll s=1; while(n){ if(n&1) s=qmul(s,a,p); a=qmul(a,a,p); n>>=1; } return s; } 快速乘 比较简单，就转化为long double 在转换为longlong 自然溢出 差
Pollard-rho算法学习笔记
weixin_34153893的博客
03-16 333
写在前面 目录 问题的提出 生日悖论 利用生日悖论来因数分解 Pollard-rho算法 例题完成进度 1/2 问题的提出 如何快速地找到一个自然数N的两个因数(除自己和1以外)？ 首先想到的肯定是传统的试除法 int main(){ int N; cin>>N; if(N%2==0){ ...
Pollard‘s Rho 算法
每行代码都热烈滚烫。
04-04 891
Pollard's Rho算法的原理剖析与实践
Pollard Rho 算法分解质数原理是什么
最新发布
08-06
<think>我们详细解释 Pollard Rho 算法用于质因数分解的原理。该算法由 John Pollard 在 1975 年提出，主要用于分解大整数的非平凡因子。其核心思想是利用一个特定的伪随机序列来生成可能因子，并通过最大公约数（GCD）检测来寻找因子。 ### 1. 算法动机 直接试除法在分解大整数时效率低下（尤其是当因子较大时）。Pollard Rho 算法利用以下观察： - 设 $n$ 为待分解的合数，$p$ 是 $n$ 的一个非平凡因子（$1<p<n$）。 - 考虑一个模 $n$ 的伪随机序列 $\{x_k\}$，如果序列模 $p$ 的值出现重复（即 $x_i \equiv x_j \pmod{p}$），那么 $|x_i - x_j|$ 将是 $p$ 的倍数。此时，计算 $\gcd(|x_i - x_j|, n)$ 可能会得到 $p$（或者 $n$ 本身，此时需调整参数重新尝试）。 然而，直接存储所有序列值并检查重复需要大量内存。Pollard Rho 算法通过 Floyd 的循环检测算法（龟兔赛跑）来高效检测循环，从而节省内存。 ### 2. 伪随机函数 通常使用一个二次函数生成伪随机序列： $$ x_{k+1} = (x_k^2 + c) \mod n $$ 其中 $c$ 是一个随机常数（通常 $c \neq 0, -2$），初始值 $x_0$ 随机选择。 ### 3. 循环检测（Floyd 方法） 设序列 $\{x_k\}$ 模 $p$ 存在循环（因为模 $p$ 的值域有限，循环必然出现）。Floyd 方法使用两个指针（龟和兔）： - 龟指针每次走一步：$t = x_i$ - 兔指针每次走两步：$h = x_{2i}$ - 当 $i$ 增加到某个值时，若 $\gcd(|t - h|, n) > 1$，则找到了一个因子。 具体步骤： 1. 初始化：$x = y = 2$（通常从2开始），$c$ 随机选择（如 $c=1$），$d = 1$。 2. 循环直到 $d \neq 1$： - $x = f(x) = (x^2 + c) \mod n$ - $y = f(f(y))$ （即 $y$ 走两步） - 计算 $d = \gcd(|x - y|, n)$ 3. 如果 $d = n$，则算法失败（需换 $c$ 重新开始）；否则 $d$ 是 $n$ 的一个因子。 ### 4. 为什么能分解？ 由于序列模 $p$ 会形成循环（形如希腊字母 $\rho$，因此得名），而模 $n$ 的序列可以看作模 $p$ 和模 $n/p$ 的组合。当两个指针在模 $p$ 下进入循环时，$|x_i - x_j|$ 是 $p$ 的倍数，因此 $\gcd(|x_i - x_j|, n)$ 至少包含因子 $p$。但若同时是 $n$ 的倍数，则得到 $d=n$（失败）。 ### 5. 算法效率 - 期望时间复杂度为 $O(n^{1/4} \log n)$，比试除法（$O(\sqrt{n})$）快得多。 - 算法是概率性的，可能失败，但可通过调整随机参数 $c$ 和 $x_0$ 重新尝试。 ### 6. 代码示例（Python） 以下是一个简化的 Pollard Rho 实现： ```python import math import random def pollard_rho(n): if n == 1: return 1 if n % 2 == 0: return 2 # 函数 f(x) = x^2 + c x = random.randint(2, n-1) y = x c = random.randint(1, n-1) d = 1 while d == 1: x = (x*x + c) % n y = (y*y + c) % n y = (y*y + c) % n # y 走两步 d = math.gcd(abs(x-y), n) if d == n: # 失败，重新选择参数 return pollard_rho(n) return d # 示例：分解 n = 10403 n = 10403 factor = pollard_rho(n) print(f"{n} 的一个因子是: {factor}") ``` ### 7. 完整质因数分解 使用 Pollard Rho 算法分解一个合数 $n$ 的完整步骤： 1. 如果 $n$ 是质数（用米勒-拉宾测试），直接输出。 2. 用 Pollard Rho 算法找到一个因子 $d$。 3. 递归分解 $d$ 和 $n/d$。 注意：实际应用中需处理小因子（如先试除小质数）以提升效率。 ### 总结 Pollard Rho 算法利用伪随机序列的循环特性和最大公约数计算，高效地寻找大整数的非平凡因子。其核心在于循环检测和随机参数调整，是一种概率算法但效率显著高于试除法[^1][^2]。 §§相关问题§§ 1. Pollard Rho 算法中如何选择随机参数 $c$ 和初始值 $x_0$ 以提高成功率？ 2. 米勒-拉宾素性测试的原理和实现细节是什么？ 3. 除了 Pollard Rho，还有哪些高效的大数分解算法（如二次筛法、数域筛法）？ 4. 如何将 Pollard Rho 算法与试除法结合进行完整的质因数分解？</think>### Pollard Rho 算法原理详解 Pollard Rho 算法是一种高效的**概率性质因数分解算法**，专门用于寻找大整数的非平凡因子（即大于1且小于整数本身的因子）。其核心思想基于**生日悖论**和**循环检测**，通过伪随机序列寻找因子。以下是逐步原理分析： --- #### 1. 算法基础：生日悖论 生日悖论指出：在 $N$ 个人中，有两人同一天生日的概率远高于直觉预期。类似地，在模 $p$（$p$ 是 $n$ 的因子）下，随机序列中两个值碰撞（$x_i \equiv x_j \pmod{p}$）的概率较高。 - 若 $x_i \equiv x_j \pmod{p}$，则 $\gcd(|x_i - x_j|, n)$ 可能是 $p$ 的倍数（即 $n$ 的非平凡因子）。 - 期望碰撞次数为 $O(\sqrt{p})$，远低于 $O(p)$，这是算法高效的关键[^1]。 --- #### 2. 伪随机序列生成 定义迭代函数生成序列： $$ f(x) = (x^2 + c) \mod n $$ 其中： - $x$ 是当前值（初始随机选择） - $c$ 是随机常数（通常 $c \neq 0, -2$） - 序列示例：$x_0, x_1 = f(x_0), x_2 = f(x_1), \dots$ 该序列在模 $n$ 下看似随机，但在模 $p$（$p|n$）下会**形成循环**（形如希腊字母 $\rho$，算法因此得名）。 --- #### 3. Floyd 循环检测 为高效检测碰撞，使用两个指针（龟兔赛跑法）： - **龟指针**（$x$）：每次移动一步，$x_{i+1} = f(x_i)$ - **兔指针**（$y$）：每次移动两步，$y_{i+1} = f(f(y_i))$ - 当 $\gcd(|x_i - y_i|, n) > 1$ 时，找到非平凡因子（可能为 $p$） ```python def pollard_rho(n): x = y = random.randint(2, n-1) # 随机初始化 c = random.randint(1, n-1) # 随机常数 d = 1 while d == 1: x = (x*x + c) % n # 龟走一步 y = (y*y + c) % n # 兔走第一步 y = (y*y + c) % n # 兔走第二步 d = math.gcd(abs(x - y), n) # 检测碰撞 return d # 返回因子 (可能是 n 本身) ``` --- #### 4. 算法步骤 1. **输入**：合数 $n$（非质数） 2. **初始化**： - 随机选择 $x, c \in [2, n-1]$ - 设 $y = x$, $d = 1$ 3. **迭代**： - $x \leftarrow f(x) = (x^2 + c) \mod n$ - $y \leftarrow f(f(y))$（移动两步） - $d \leftarrow \gcd(|x - y|, n)$ 4. **终止条件**： - 若 $d > 1$，返回 $d$（找到因子） - 若 $d = n$，失败（需换 $c$ 重试） 5. **递归分解**：对因子 $d$ 和 $n/d$ 递归调用算法 --- #### 5. 数学原理 设 $p$ 是 $n$ 的最小质因子： - 序列 $\{x_k \mod p\}$ 会进入循环（值域有限） - 龟兔指针在 $O(\sqrt{p})$ 步内以高概率碰撞（生日悖论） - 碰撞时 $x_i \equiv y_i \pmod{p}$，故 $|x_i - y_i|$ 含因子 $p$ - $\gcd(|x_i - y_i|, n)$ 至少包含 $p$（除非是 $n$ 本身） --- #### 6. 时间复杂度 - **期望复杂度**：$O(n^{1/4} \log n)$ - **优势**：比试除法（$O(\sqrt{n})$）快指数级 - **概率性**：可能失败，但可通过调整 $c$ 和 $x_0$ 重试 --- #### 7. 完整分解示例（Python） ```python import math import random def is_prime(n): """米勒-拉宾素性测试（简化版）""" if n < 2: return False for p in [2, 3, 5, 7, 11]: if n % p == 0: return n == p return True # 简化处理 def pollard_rho(n): if n % 2 == 0: return 2 x = random.randint(2, n-1) y = x c = random.randint(1, n-1) d = 1 while d == 1: x = (x*x + c) % n y = (y*y + c) % n y = (y*y + c) % n d = math.gcd(abs(x - y), n) if d == n: return pollard_rho(n) # 失败重试 return d def factorize(n): if is_prime(n) or n == 1: return [n] d = pollard_rho(n) return factorize(d) + factorize(n//d) # 分解 n = 10403 (101×103) print(factorize(10403)) # 输出: [101, 103] ``` --- ### 关键点总结 1. **随机性**：$c$ 和初始值 $x$ 随机选择，避免死循环。 2. **碰撞检测**：龟兔赛跑法以 $O(1)$ 空间检测循环。 3. **递归分解**：对找到的因子递归调用，直到得到质因子。 4. **效率**：特别适合分解含中等大小因子的大整数（如 RSA 模数）[^1][^2]。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值