AP聚类算法（Affinity propagation Clustering Algorithm ）

     AP聚类算法是基于数据点间的"信息传递"的一种聚类算法。与k-均值算法或k中心点算法不同，AP算法不需要在运行算法之前确定聚类的个数。AP算法寻找的"examplars"即聚类中心点是数据集合中实际存在的点，作为每类的代表。

 

算法描述：

   假设$\{ {x_1},{x_2}, \cdots ,{x_n}\} $数据样本集，数据间没有内在结构的假设。令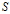是一个刻画点之间相似度的矩阵，使得$s(i,j) > s(i,k)$当且仅当$x_i$与$x_j$的相似性程度要大于其与$x_k$的相似性。

AP算法进行交替两个消息传递的步骤，以更新两个矩阵：

• 吸引信息（responsibility）矩阵R：$r(i,k)$描述了数据对象k适合作为数据对象i的聚类中心的程度，表示的是从i到k的消息；
• 归属信息（availability）矩阵A：$a(i,k)$描述了数据对象i选择数据对象k作为其据聚类中心的适合程度，表示从k到i的消息。

 

    两个矩阵R ,A中的全部初始化为0. 可以看成Log-概率表。这个算法通过以下步骤迭代进行：

• 首先，吸引信息（responsibility）${r_{t + 1}}(i,k)$按照

${r_{t + 1}}(i,k) = s(i,k) - \mathop {\max }\limits_{k' \ne k} \{ {a_t}(i,k') + s(i,k')\} $

的迭代。

• 然后，归属信息（availability）${a_{t + 1}}(i,k)$按照

\[{a_{t + 1}}(i,k) = \mathop {\min }\limits_{} \left( {0,{r_t}(k,k) + \sum\limits_{i' \notin \{ i,k\} } {\max \{ 0,{r_t}(i',k)\} } } \right),i \ne k\]

和

\[{a_{t+1}}(k,k) = \sum\limits_{i' \ne k} {\max \{ 0,{r_t}(i',k)\} } \]

迭代。

• 对以上步骤进行迭代，如果这些决策经过若干次迭代之后保持不变或者算法执行超过设定的迭代次数，又或者一个小区域内的关于样本点的决策经过数次迭代后保持不变，则算法结束。

 

    为了避免振荡，AP算法更新信息时引入了衰减系数$\lambda $。每条信息被设置为它前次迭代更新值的$\lambda $倍加上本次信息更新值的1-$\lambda $倍。其中，衰减系数$\lambda $是介于0到1之间的实数。即第t+1次$r(i,k)$，$a(i,k)$的迭代值：

\[{r_{t + 1}}(i,k) \leftarrow (1 - \lambda ){r_{t + 1}}(i,k) + \lambda {r_t}(i,k)\]

\[{a_{t + 1}}(i,k) \leftarrow (1 - \lambda ){a_{t + 1}}(i,k) + \lambda {a_t}(i,k)\]

 

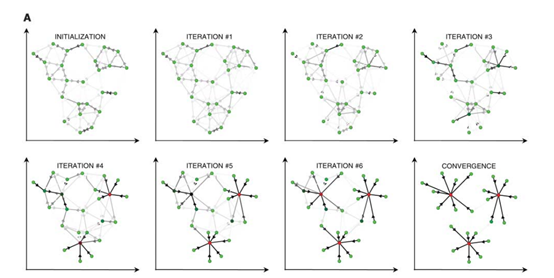
图1 算法实现过程

 

图2 对人脸数据库的聚类结果比较

 

 

转载于:https://www.cnblogs.com/huadongw/p/4202492.html