折半搜索法 - 迭代

在正式进入主题之前，对于上一次用递归实现的折半搜索法，这里分析一下它的空间复杂度，在面试做笔记题的时候也是经常会被问到，先贴出上次的实现：

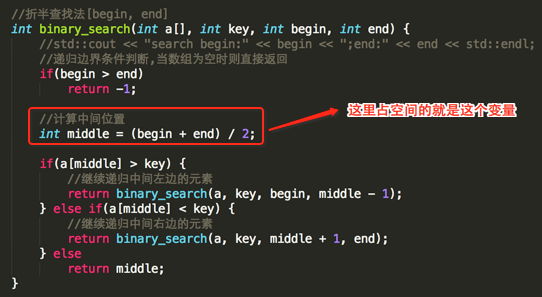
我们知道总的递归产生的时间复杂度是O(log n)，而这么多次递归中每次都会有一个middle，也就是有log n个middle,所以说它的空间复杂度S(n) = O(log n)，也就是随着N的不断增加，相应的空间也会增加。

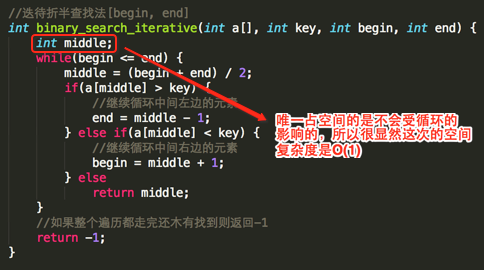
那么有木有不需要middle这个变量让其空间复杂度更小的实现方式呢【对于面试来说假如已经你已经实现了用递归实现折半，面试官问你那还有优化的方案么，这就相当于是优化方案】？于是乎也就是今天要引入的正题----通过迭待来实现，可以基于递归的思想稍加改良既可，如下：

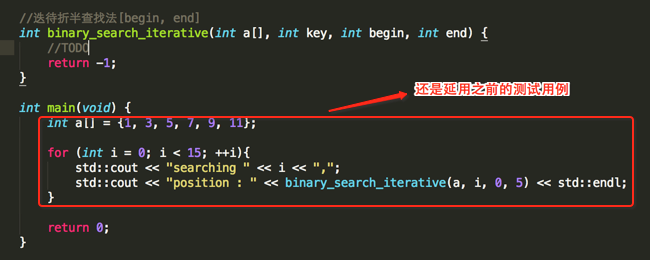
下面开始实现：

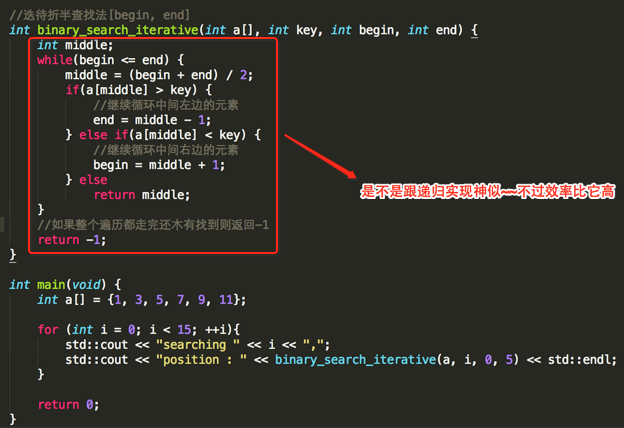
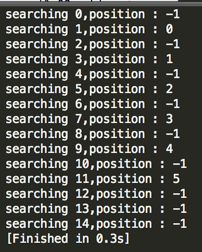
编译运行：

那下面分析一下这种实现的空间复杂度：

转载于:https://www.cnblogs.com/webor2006/p/7190453.html