第三次作业

2.利用程序huff_enc和huff_dec进行以下操作（在每种情况下，利用由被压缩图像生成的码本）。

（a）对Sena,Sensin和Omaha图像进行编码。

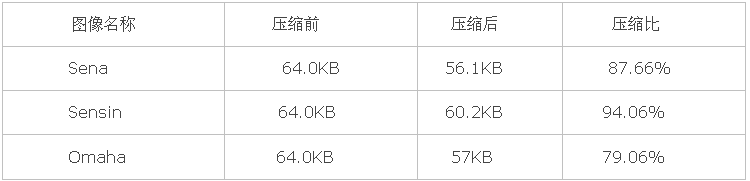
所以压缩率一般是越小越好，但是压得越小，解压时间就越长。

4.一个信号源从符号集A={a₁,a₂,a₃,a_4,a₅}中选择字母,其概率为P(a₁)=0.15, P(a₂)=0.04, P(a₃)=0.26, P(a₄)=0.05, P(a₅)=0.50.

(a)计算这个信源的熵。

H(A)=-P(a₁)log₂P(a1)-P(a₂)log₂P(a₂)-P(a₃)log₂P(a₃)-P(a₄)log₂P(a₄)-P(a₅)log₂P(a₅)

         = -0.15*log₂0.15-0.04*log₂0.04-0.26*log₂0.26-0.05*log₂0.05-0.50*log₂0.50

         =0.15* 2.737+0.04*4.644+0.26*1.943+0.05*4.322+0.5*1

         =0.411+0.186+0.505+0.216+0.5

         =1.818（bits/symbol）         

(b)求这个信源的霍夫曼码。

          a1的编码为：001

          a2的编码为：0000

          a3的编码为：01

          a4的编码为：0001

          a5的编码为：1

(c)求(b)中代码的平均长度及其冗余度。

平均长度：L=P(a₁)*L1+ P(a₂)*L2+P(a₃)*L3+P(a₄)*L4+P(a₅)*L5

                   =0.15*3+0.04*4+0.26*2+0.05*4+0.5*1

                   =0.45+0.16+0.52+0.2+0.5

                   =1.83（bits/symbol）

 冗余度：L-H(A)=1.83-1.818=0.012（bits/symbol）

转载于:https://www.cnblogs.com/yangnana/p/5888026.html