Third Maximum Number

　　　　这道题为简单题

　　题目：

　　　　

 

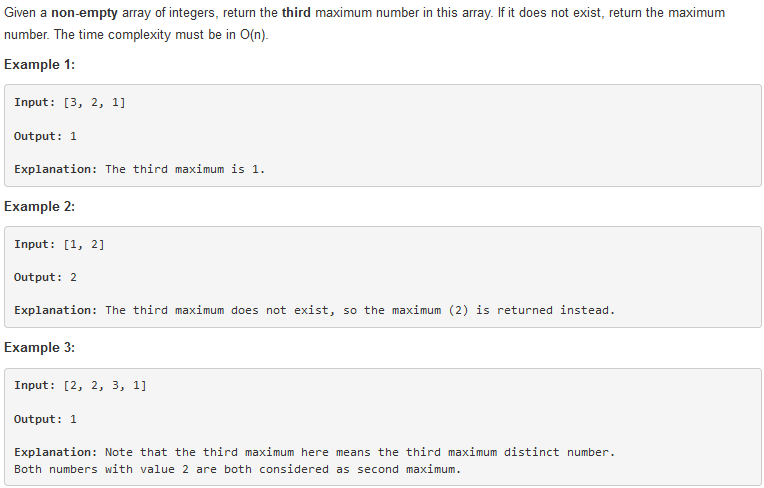
　　思路：

　　　　我直接设置三个变量分别储存前三大值，遍历整个列表，然后就是与三个值分别比较，并且每次num += 1，如果最后num大于3，那么说明前三大值存在，返回f3，否则不存在返回f1

　　代码：　

 1 class Solution(object):
 2     def thirdMax(self, nums):
 3         """
 4         :type nums: List[int]
 5         :rtype: int
 6         """
 7         f1 = float('-Inf')
 8         f2 = float('-Inf')
 9         f3 = float('-Inf')
10         num = 0
11         for i in nums:
12             if i > f1:
13                 f3 = f2
14                 f2 = f1
15                 f1 = i
16                 num += 1
17             elif f1 > i and i > f2:
18                 f3 = f2
19                 f2 = i
20                 num += 1
21             elif f2 > i and i > f3: 
22                 f3 = i
23                 num += 1
24         if num < 3: return f1
25         else: return f3

 

转载于:https://www.cnblogs.com/liuxinzhi/p/7571539.html