《University Calculus》-chaper13-向量场中的积分-线积分

  线积分：

  基于二重积分和三重积分的引入，我们对于线积分的引入过程将会轻车熟路。

 

  对于一根不均匀密度的铜丝，我们如何求其总质量？如下图。

 

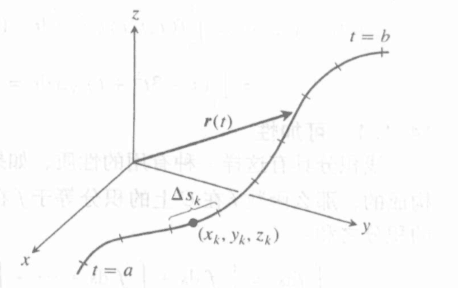
  类似二重积分和三重积分的引入，我们首先基于实际问题给出黎曼和的形式，然后规定出积分符号，然后抽象出模型，然后再讨论如何正确的计算。

  这里我们将这段曲线分割成n个区间段，可以近似求解质量，而随着n趋向无穷，这种近似的取法最终将逼近准确答案，则有如下的黎曼和形式(这里建立三维坐标系，f(x,y,z)是记录铜导线(x,y,z)点的密度的函数)：

                           

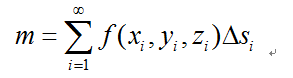
  写成积分形式为：

 

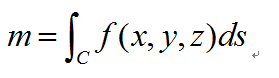
  其表示函数f(x,y,z)在曲线C上的线积分。

 

转载于:https://www.cnblogs.com/rhythmic/p/5657189.html