一元二次方程

ax²+bx+c=0（a≠0），其中  是二次项，  是二次项系数；  是一次项；  是一次项系数；  是常数项。

使方程左右两边相等的未知数的值就是这个一元二次方程的解，一元二次方程的解也叫做一元二次方程的根

 

 参考：百度百科

---

 

-------一元二次方程的解（根）--------

ax²+bx+c=0（a≠0）

-----------------------------------------------------------

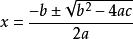
 据判别式计算有几个根：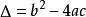

① 当   时，方程有两个不相等的实数根；

② 当   时，方程有两个相等的 实数根；

③ 当   时，方程无实数根，但有2个 共轭复根。

上述结论反过来也成立。

---------------------------------------------------------

韦达定理（两根关系）

设一元二次方程     中，两根   有如下关系：

　　

　　

 

推导如下：

由一元二次方程求根公式知： 

则有：

 

 

---

 

一元二次方程变形式

 （  是实数，  ）

 （   是实数，   ）

 

 

 （是实数）

--------------------------------------------------

配方式

 

----------------------------------------------------

两根式

 

-------------------------------------------------------

转载于:https://www.cnblogs.com/chenxi188/p/11106632.html