Grundlegendes Wort:
矩阵列:Das Spalte von der Matrix
行列式:Die Determinante
对角矩阵:Die diagonal Matrix
逆矩阵:Die inverse Matrix
可逆矩阵:Die reguläre Matrizen
线性:Linear
线性组合:DIe Linearkombination
线性方程组:Die Lineare Gleichung
矩阵求逆:Matrix invertierbar
矩阵乘法:Die Matrizenmultiplikation
矩阵的减法:Die Matrizensubstraktion
矩阵加法:Die Matrizenaddition
不可逆矩阵:Die singulär Gleichung
矩阵的转置:Die Transportierung der Matrix
转置矩阵:Die Transponierte Matrix
Determinante

Matrix
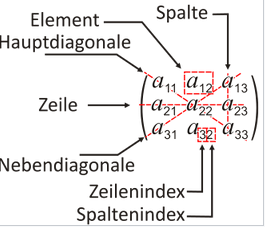
In der Mathematik versteht man unter einer Matrix eine rechteckige Anordnung von Elementen
Matrizenaddition
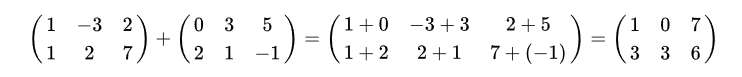
Skalarmultiplikation
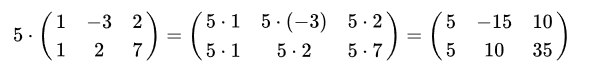
Matrizenmultiplikation
Zwei Matrizen können multipliziert werden, wenn die Spaltenanzahl der linken mit der Zeilenanzahl der rechten Matrix übereinstimmt.
l×m Matrix und m×n Matrix ist eine l×n Matrix
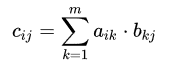
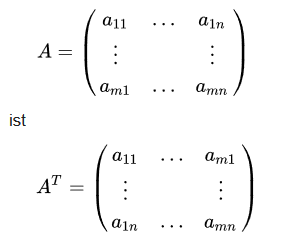
Transponierte Matrix
Inverse Matrix
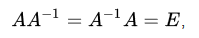
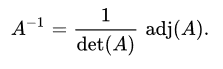
Minor
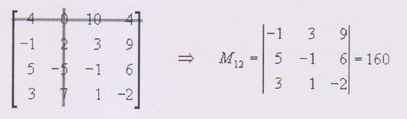
Algebraischer Minor
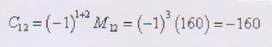
Beispiel

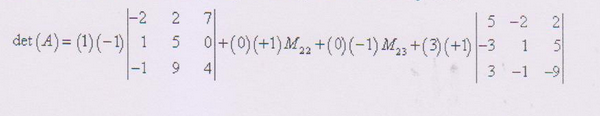
Cramer's rule
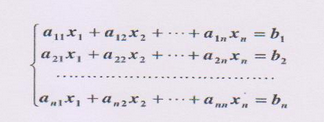
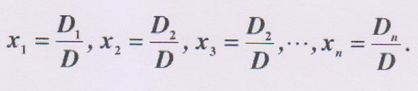
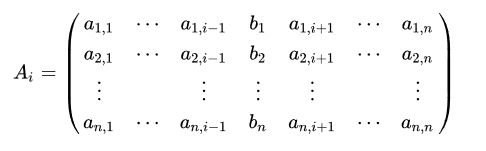







 本文深入讲解了矩阵的基础概念,包括行列式、对角矩阵、逆矩阵等,并探讨了矩阵的运算如加法、减法、乘法及转置,特别强调了矩阵在数学中的重要作用。
本文深入讲解了矩阵的基础概念,包括行列式、对角矩阵、逆矩阵等,并探讨了矩阵的运算如加法、减法、乘法及转置,特别强调了矩阵在数学中的重要作用。
















 182
182

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








