【DP】洛谷 P1854 花店橱窗布置

最新推荐文章于 2024-04-09 09:22:59 发布

转载最新推荐文章于 2024-04-09 09:22:59 发布 · 210 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/qxyzili--24/p/10425901.html

文章标签：

#数据结构与算法

本文介绍了一种使用动态规划解决P1854题目的方法，通过定义状态f[i][j]为第i束花插在第j个花瓶里的最大美学值，推导出状态转移方程，并提供了AC代码。

　　你们好啊，我又回来了。P1854这是一道动态规划题。

　　还是先放题目，防止走错》》》

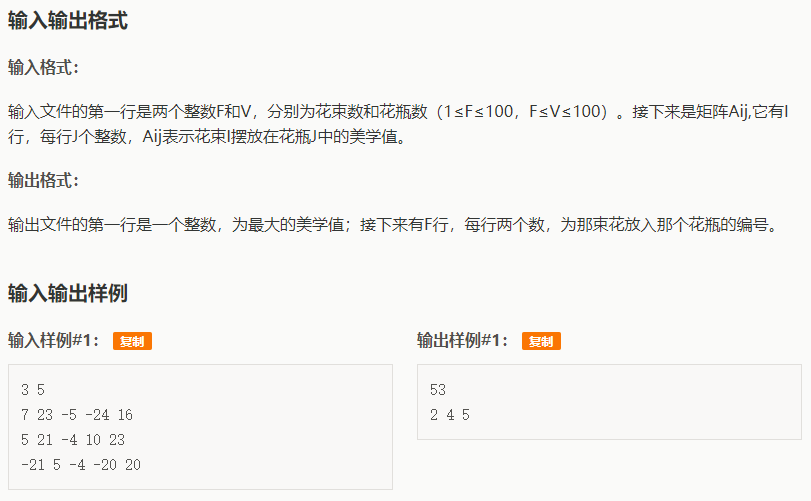
这次先放数据，上次就忘了..........

　　其实我们看见数据只有100，其实就可以考虑瞎搞，什么记忆化搜索，题解还有人求最长路，闲的无聊你可以自己尝试。

　　我这里介绍一下这题正解 -> dp。

　　其实很显然的吧........

　　这个题，我们考虑我们考虑用

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;

int f,v,ans;
int z[101][101],g[101][101],b[101][101];
//表示，前i的花放在前j的瓶；在 g中i-1的位置 
int d[101];

int main()
{
    scanf("%d%d",&f,&v);
    for(int i=1;i<=f;i++)
        for(int j=1;j<=v;j++) 
            scanf("%d",&z[i][j]);
    for(int i=1;i<=v-f+1;i++) g[1][i]=z[1][i];
    for(int i=2;i<=f;i++) 
        for(int j=i;j<=v-f+i;j++)//第j个 
            for(int k=i-1;k<=j-1;k++)//第i-1束花的位置
                if(g[i-1][k]+z[i][j]>g[i][j])
                {
                    g[i][j]=g[i-1][k]+z[i][j];
                    b[i][j]=k;//等候i-1 
                }
    int sum=0,max=-2147483647;
    for(int i=f;i<=v;i++) {
        if(g[f][i]>max) {
            max=g[f][i];
            sum=i;
        }
    }
    cout<<max<<endl;
    for(int i=1;i<=f;i++)  {
        d[i]=sum;
        sum=b[f-i+1][sum];
    }
    for(int i=f;i>=1;i--) cout<<d[i]<<endl;
    return 0;
}