树

树

为什么要有树？

线性结构中存在问题：查找 和 插入 操作的繁琐

二叉树

1.链式存储的二叉树

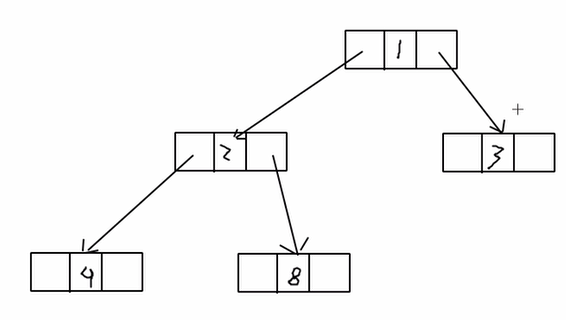
遍历 、查找、 删除

package 二叉树;

public class 二叉树 {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        
        //创建一棵树
        binarytree bintree=new binarytree();
        //创建根节点
        treenode root=new treenode(1);
        //根节点赋给树
        bintree.setRoot(root);
        //创建两个节点
        treenode l=new treenode(2);
        treenode r=new treenode(3);
         root.setLefTreenode(l);
         root.setRighTreenode(r);
         
         l.setLefTreenode(new treenode(4));
         l.setRighTreenode(new treenode(5));
         
         r.setLefTreenode(new treenode(6));
         r.setRighTreenode(new treenode(7));
         //前序遍历树
         bintree.frontshow(); 
         //前序查找
         treenode  resulTreenode=bintree.frontsearch(5);
         System.out.println(resulTreenode );
         //删除1个子树
         bintree.delete(2);
         bintree.frontshow();
    }
}

package 二叉树;

public class binarytree {
    treenode root;

    public treenode getRoot() {
        return root;
    }

    public void setRoot(treenode root) {
        this.root = root;
    }
    public void frontshow() {
        root.frontshow();
    }
    public treenode frontsearch(int i) {
        return root.frontsearch(i);
    }

    public void delete(int i) {
        // TODO Auto-generated method stub
        if(root.value ==i) {
            root=null;
        }else {
            root.delete(i);
        }
    }
}

package 二叉树;

public class treenode {
    int value;
    treenode lefTreenode;
    treenode righTreenode;
    public treenode(int value) {
        this.value=value;
    
    }
    public treenode getLefTreenode() {
        return lefTreenode;
    }
    public void setLefTreenode(treenode lefTreenode) {
        this.lefTreenode = lefTreenode;
    }
    public treenode getRighTreenode() {
        return righTreenode;
    }
    public void setRighTreenode(treenode righTreenode) {
        this.righTreenode = righTreenode;
    }
    //前序遍历
    public void frontshow() {
        // TODO Auto-generated method stub
        System.out.println(value);
        if(lefTreenode !=null) {
            lefTreenode.frontshow();
        }
        if(righTreenode !=null) {
            righTreenode.frontshow();
        }
    }
    public treenode frontsearch(int i) {
        // TODO Auto-generated method stub
        //对比当前值
        treenode target =null;
        //先对比当前值
        if(this.value==i) {
            return this;
        }else {
            //再对比左节点的值
            if(lefTreenode !=null) {
                target=lefTreenode.frontsearch(i);
            }
            //如果target不为空，就说明找到了。
            if(target!=null) {
                return target;
            }
            if(righTreenode !=null) {
                target =righTreenode.frontsearch(i);
            }
        }
        return target;
    }
    
    //删除子树
    public void delete(int i) {
        // TODO Auto-generated method stub
        treenode parenTreenode=this;
        //判断左儿子
        if(parenTreenode.lefTreenode!=null&&parenTreenode.lefTreenode.value==i) {
            parenTreenode.lefTreenode=null;
            return;
        }
        if(parenTreenode.righTreenode!=null&&parenTreenode.righTreenode.value==i) {
            parenTreenode.righTreenode=null;
            return;
        }
        //递归检查左儿子
        parenTreenode=lefTreenode ;
        if(parenTreenode !=null) {
            parenTreenode.delete(i);
        }
        parenTreenode=righTreenode  ;
        if(parenTreenode !=null) {
            parenTreenode.delete(i);
        }
    }
}

2.顺序存储的二叉树

 顺序存储的二叉树通常情况只考虑完全二叉树。因为对于其他二叉树而言，不能满足顺序存储的结果。

 性质

对于第n个元素的左子节点是2*n+1;右子节点2*n+2；父节点（n-1）/2；（可用于遍历操作）

遍历

package 二叉树;

public class arraybinarytree {
    int[] data;

    public arraybinarytree(int[] data) {
        super();
        this.data = data;
    }
    //前序遍历顺序存储的二叉树
    public void frontshow(int index) {
        if(data==null||data.length==0)return;
        //先遍历当前节点
        System.out.println(data[index]);
        //左子树  2*index+1
        if(2*index+1<data.length)frontshow(2*index+1);
        if(2*index+2<data.length)frontshow(2*index+2);
    }
}

堆排序

升序->大顶堆

堆是一颗完全二叉树。

堆排序的思想：

1.将初始待排关键字序列构建成大顶堆；（初始堆：从最后1个非叶子节点开始调整）

2.将堆顶元素与最后1个元素进行交换，得到新的无序区（r1...r_（n-1））和有序区r_n

3.由于交换后新的堆顶可能违反堆的性质，再将无序区调整为新堆，将r1与无序区的的最后1个元素交换，得到新的

无序区（r1...r_（n-2））和有序区（r_n-1,r_n）,不断重复。

package 堆;

import java.lang.reflect.Array;
import java.util.Arrays;

public class heap {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] arr=new int[] {9,6,8,7,0,1,10,4,2};
        //从最后1个非叶子节点开始调整，也就是最后1和叶子节点的父节点
        int start=(arr.length-1)/2;
        //结束位置 数组的长度-1；
        for(int  i=start;i>=0;i--) {
            maxheap(arr, arr.length, i);
        }
        System.out.println(Arrays.toString(arr));
    }
    //size加入堆的元素个数,防止越界
    //排序
    public static void heapsort(int[] arr) {
        int start=(arr.length-1)/2;
        for(int  i=start;i>=0;i--) {
            maxheap(arr, arr.length, i);
        }
        //调整为大顶堆
        for(int i=arr.length-1;i>0;i--) {
            int tmp=arr[0];
            arr[0]=arr[i];
            arr[i]=tmp;
            maxheap(arr, i, 0);
        }    
    }
    
    
    
    public static void maxheap(int[] arr, int size, int index) {
        //左子节点
        int leftnode=2*index+1;
        int rightnode=2*index+2;
        int max=index;
        if(leftnode<size&&arr[leftnode]>arr[max]){
            max=leftnode;
        }
        if(leftnode<size&&arr[rightnode]>arr[max]){
            max=rightnode;
        }
        //交换位置
        if(max!=index) {
            int tmp=arr[index];
            arr[index]=arr[max];
            arr[max]=tmp;
            //交换位置之后，可能会破坏之前排好的堆，所以，之前排好的堆要重新调整
            maxheap(arr, size, max);
        }
    }

}

 线索二叉树

线索化：前序 中序  后序化

赫夫曼树

最优二叉树。n个带权叶子结点构成的所有二叉树中，带权路径最小的二叉树。

叶结点的带权路径：从根节点开始到叶子节点路径中经过的节点（不包括叶子节点）乘以叶子节点的权值。

树的带权路径长度wpl:所有叶子节点带权值之和。

wpl最小的树为赫夫曼树。（权值大的节点离根节点尽量近）

赫夫曼编码步骤：

统计字符数并排序

（取出根节点权值最小的两颗二叉树

组成1颗新的二叉树

根节点权值是前面两颗二叉树权值之和

重复以上步骤）

创建赫夫曼树

赫夫曼编码表

赫夫曼编码

非定长编码：

前缀编码：字符的编码都不能是其他字符编码的前缀。

赫夫曼编码：

 

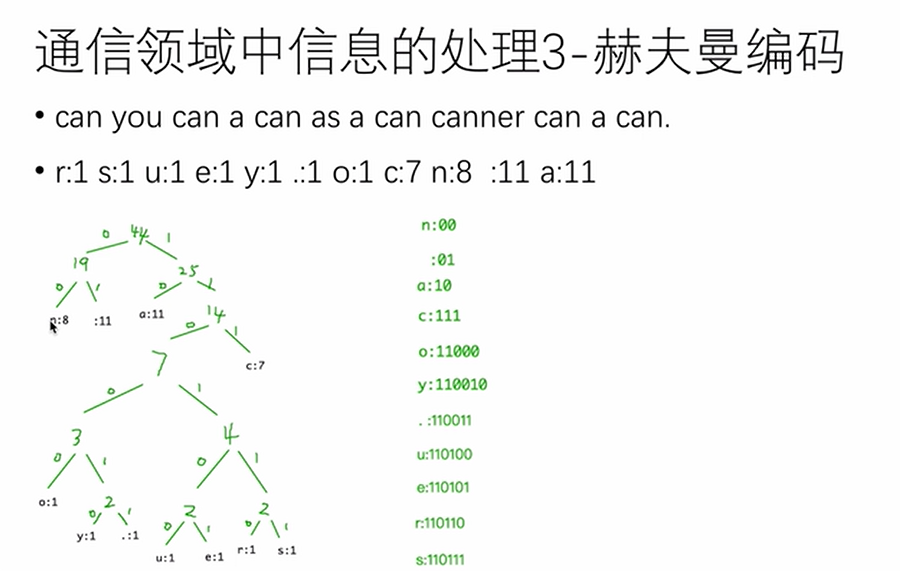
 不会出现不满足前缀编码的问题，每个字母对应的路径是唯一的。

 

 二叉排序树BST

方便查找 删除

缺点：左斜或者右斜

 平衡二叉树AVL

 前提：是1颗二叉排序树。左子树和右子树高度差不超过1.

优点：查找效率比较高。

计算机中数据的存储原理

多路查找树（2-3树和2-3-4树   B树和B+树）

 磁盘的预读：

由于磁盘的读写速度问题，要尽量减少磁盘io操作，所以磁盘往往不是严格按需读取，而是每次都会预读，即使只需要1个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据到内存，也就是局部性原理。

预读的长度一般是页page的整数倍。

页：1个存储块，4K.

文件系统利用磁盘预读原理，将1个节点的大小设为1个页的大小，这样每个节点只需要1次io。

二叉树：当数据量非常大时，二叉树的高度会很高；另一方面，每读取1个节点进行1次io操作，消耗性能。

改进：B树。

 

2-3树（B树的一种）

二节点：有两个子节点的节点

三节点：有三个子节点的节点

二节点要么有两个子节点，要么没有；三节点要么有三个子节点，要么没有。

 

红黑树

也是二分查找树。

根节点是黑色的，每个叶子节点（最后的空节点）是黑色的，如果1个节点是红色的，那么他的孩子都是黑色的。

从任意1个节点到叶子节点，经过的黑色节点是一样的。

（理解：2-3树任意1个节点到某节点经过的节点树一定相同，而2节点和3节点转化为红黑树时都会有1个黑节点，等价性）

Donald Knuth 计算机编程的艺术

红黑树与2-3树的等价性

2-3树

　　满足二分查找树的基本性质

　　节点可以存放1个或者两个元素

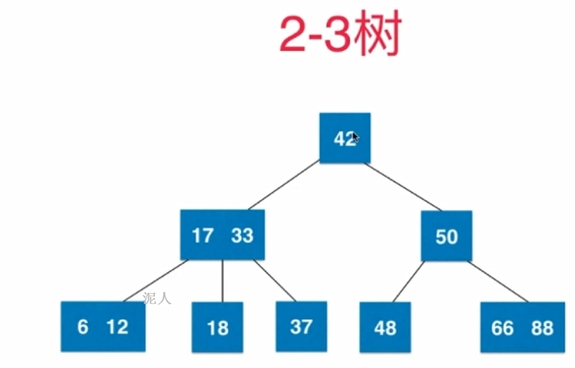
　　2-3树是一颗绝对平衡的树。

       2-3是如何维持绝对平衡的？

　　如果插入2节点，就变成3节点；如果插入3节点，就暂时变成4节点，然后进行拆解变形。，保持平衡性。

 　　

 

 

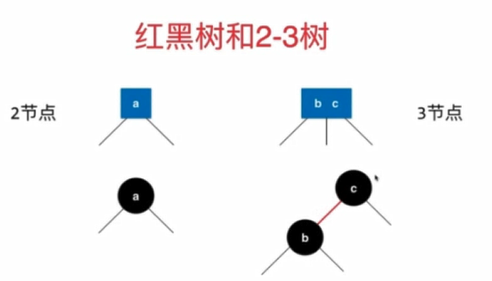
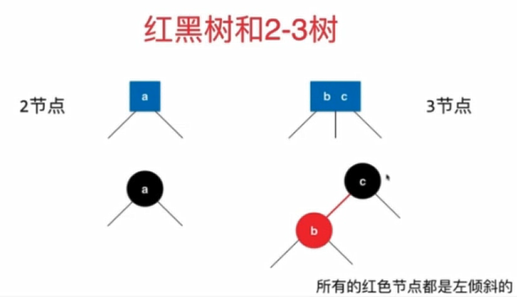
 红黑树时保持黑平衡的二叉树，严格意义上讲，不是平衡二叉树。所以在查找性能上，红黑树会慢于平衡二叉树。

但是添加或者删除，性能更高。

最大高度：2lonn  遍历时间复杂度：o(logn)

 

应用场景：

	应用场景
B树	数据库和文件系统。(将相关数据尽量集中在一起，1次读取多个数据，减少磁盘IO)
B+树	mysql索引（每个关键字不保存数据，只用来索引，数据保存在叶子节点中）（叶子节点存放记录以链表形式连接，范围查找和查询效率高）
红黑树	搜索时，插入删除次数多时代替AVL：java中的treemap；linux进程调度，管理进程控制块
AVL	适合插入删除少，查询多的情况：windows对进程地址空间的管理。

AV树是严格维持平衡的，但是维持平衡本身需要额外的操作，加大了数据结构的时间复杂度；二叉搜索树可能会变成左斜或者右斜。综合以上两者，红黑树可以理解为AVL和二叉搜索树的折中：尽量维持数的平衡，又不花过多的时间维持数据结构的性质。

 

B+树相对B树的优点：

①B+树的所有Data域在叶子节点，一般来说都会进行一个优化，就是将所有的叶子节点用指针串联起来，遍历叶子节点就能获取全部数据，这样就能进行区间访问了。

②IO一次读数据是从磁盘上读的，磁盘容量是固定的，取数据量大小是固定的，非叶子节点不存储数据，节点小，磁盘IO次数就少。

B树：平衡树。

关键字集合分布在整棵树中；

搜索性能等价于在关键字全集内做二分查找。

B+树：

所有数据放在叶子节点的链表中，并且链表中的关键字也是有序的；

不可能在非叶子节点命中；

非叶子节点相当于是叶子节点的索引；更加适合文件索引系统。

 

转载于:https://www.cnblogs.com/NeverGiveUp0/p/11159179.html