第二次作业

2 利用程序huff_enc和huff­_dec进行以下操作（在每种情况下，利用由被压缩图像生成的码本）。

（a） 对Sena、Sensin和Omaha图像时行编码。

图像	压缩前	压缩后	压缩比
SENA	64kb	57kb	0.89
OMAHA	64kb	58kb	0.90
SINAN	64kb	61kb	0.95

 

 

 

 

（b） 编写一段程序，得到相邻之差，然后利用huffman对差值图像进行编码。

 

 

4 一个信源从符号集A={a₁, a₂, a₃, a₄, a₅}中选择字母，概率为P（a₁）=0.15=3/20，P（a₂）=0.04=1/25，P（a₃）=0.26=13/50，P（a₄）=0.05=1/20，P（a₅）=0.50=1/2。

（a）计算这个信源的熵。

（b）求这个信源的霍夫曼码。

（c）求（b）中代码的平均长度及其冗余度。

        (a)

H（a）=-∑P(x)logP(x) 

        =0.15*log₂20/3 + 0.04*log₂25+ 0.26*log₂50/13+0.05*log₂20 +0.5*log₂2

 

   (b)

先将其排序（升序）

a₅   0.50

a₃   0.26

a₁   0.15

a₄    0.05

a₂    0.04

 

 

 

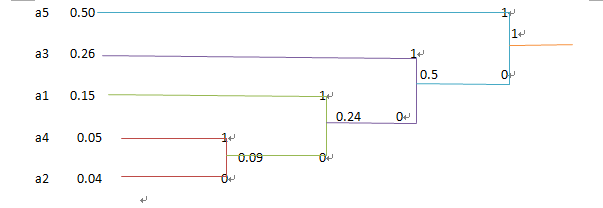
(c)

平均长度=0.15*3+0.04*4+0.26*2+0.05*4+0.5*1=1.83bits

冗余度=平均长度-H(a)=1.83-1.8=0.03bits

5  一个符号集A={a₁, a₂, a₃, a₄,}，其概率为P（a₁）=0.1，P（a₂）=0.3，P（a₃）=0.25，P（a₄）=0.35，使用以下过程找出一种霍夫曼码：

（a）本章概述的第一种过程：

（b）最小方差过程。

  解释这两种霍夫曼码的区别。

（a）

P	霍夫曼码
a1（ 0.1）	110
a2（ 0.3）	10
a3（ 0.25）	111
a4（ 0.35）	0

 

 

 

 

 

（b） 

P	霍夫曼码
a1（ 0.1）	00
a2（ 0.3）	10
a3（ 0.25）	01
a4（ 0.35）	11

  

 

 

 

 

 

参考书《数据压缩导论（第4版）》Page 30

6在本书配套的数据中有几个图像和语音文件。

(a) 编写一段程序，计算其中一些图像和语音文件的一阶熵。

(b) 选择一个图像文件，计算其二阶熵。试解释一阶熵与二阶熵的差别。

(c) 对于(b)中所有的图像文件，计算其相邻像素之差的熵，试解释你的发现。

图像	一阶熵	二阶熵	差熵
EARTH	4.770801	2.568358	3.962697
OMAHA	6.942426	4.488626	6.286834
SENA	6.834299	3.625204	3.856989
SENSIN	7.317944	4.301673	4.541547
BERK	7.151537	6.705169	8.976150
GABE	7.116338	6.654578	8.978236

 

 

 

 

 

 

 

 

 （1）以上三个文件都是图片类型的文件，也就是说它们的文件类型相同，并且它们的文件大小也相同，但是从表格中可以看出，文件类型、文件大小相同的文件，它们的一阶熵、二阶熵、差分熵并不一定相同。

（2）一阶熵与二阶熵相差近似为3 ，差熵与一阶熵相差不大。

转载于:https://www.cnblogs.com/nieguilin/p/4800480.html