堆与堆排序

最新推荐文章于 2023-05-28 11:19:59 发布

转载最新推荐文章于 2023-05-28 11:19:59 发布 · 93 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/spirals/archive/2010/09/14/1825516.html

1.什么是堆

这里的堆（二叉堆），指得不是堆栈的那个堆，而是一种数据结构。

堆可以视为一棵完全的二叉树，完全二叉树的一个“优秀”的性质是，除了最底层之外，每一层都是满的，这使得堆可以利用数组来表示（普通的一般的二叉树通常用链表作为基本容器表示），每一个结点对应数组中的一个元素。

如下图，是一个堆和数组的相互关系

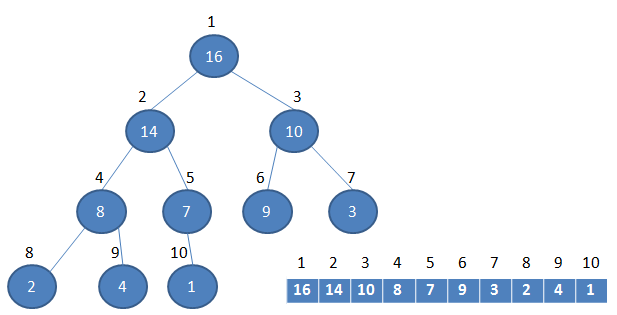
二叉堆一般分为两种：最大堆和最小堆。两种堆内部的数据都要满足自己的特点。

比如最大堆的特点是，每个父节点的元素值都不小于其孩子结点（如果存在）的元素值，因此，最大堆的最大元素值出现在根结点（堆顶）

最小堆的性质与最大堆恰好相反

由于堆排序算法使用的是最大堆，所以我们这里以最大堆为例，最小堆情况类似，可以自己推导

对于给定的某个结点的下标i，可以很容易的计算出这个结点的父结点、孩子结点的下标，而且计算公式很漂亮很简约

$gif.latex?%5C120dpi%20%20PARENT%5Cleft%20(%20i%20%5Cright%20)=%5Cleft%20%5Clfloor%20%5Cfrac%7Bi%7D%7B2%7D%20%5Cright%20%5Crfloor%20%5C%5C%20%5Cindent%20LEFT%5Cleft%20(%20i%20%5Cright%20)=2i%20%5C%5C%20%5Cindent%20RIGHT%5Cleft%20(%20i%20%5Cright%20)=2i+1$

但是这里有一个很大的问题：目前主流的编程语言中，数组都是Zero-based，这就意味着我们的堆数据结构模型要发生改变

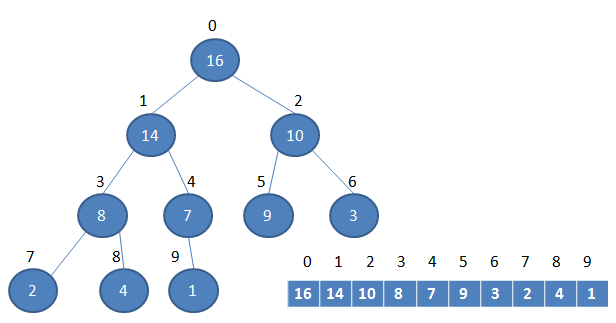
相应的，几个计算公式也要作出相应调整

$gif.latex?%5C120dpi%20PARENT%5Cleft%20(%20i%20%5Cright%20)=%5Cleft%20%5Clfloor%20%5Cfrac%7Bi+1%7D%7B2%7D%20%5Cright%20%5Crfloor%20-1%5C%5C%20%5Cindent%20LEFT%5Cleft%20(%20i%20%5Cright%20)=2i+1%20%5C%5C%20%5Cindent%20RIGHT%5Cleft%20(%20i%20%5Cright%20)=2%5Cleft%20(i+1%20%5Cright%20)$

新公式很难看，很杯具

这几个公式在C/C++中可以用宏或者内联函数实现

 
    1#define LEFT(x) ((x << 1) + 1) 

    2#define RIGHT(x) ((x + 1) << 1) 

    3#define PARENT(x) (((x + 1) >> 1) - 1)

2.堆排序

堆排序是一种利用堆这种数据结构，进行原地排序的排序算法，其时间复杂度是O(nlogn)，而且只和数据规模有关

堆排序算法是一种很漂亮的算法，这里需要用到三个函数：MaxHeapify、BuildMaxHeap和HeapSort

2.1MaxHeapify

MaxHeapify的作用是保持最大堆的性质，是整个排序算法的核心。

MaxHeapify函数接受三个参数，数组，检查的起始下标和堆大小。函数的代码如下

 
    01/* 

    02    输  入: Ary(int[]) - [in,out]排序数组 

    03            nIndex(int) - 起始下标 

    04            nHeapSize(int) - 堆大小(zero-based) 

    05    输  出: - 

    06    功  能: 从nIndex开始检查并保持最大堆性质 

    07*/

    08void MaxHeapify(int Ary[], int nIndex, int nHeapSize) 

    09{ 

    10    int nL = LEFT(nIndex); 

    11    int nR = RIGHT(nIndex); 

    12    int nLargest; 

    13  

    14    if (nL <= nHeapSize && Ary[nIndex] < Ary[nL]) 

    15    { 

    16        nLargest = nL; 

    17    } 

    18    else

    19    { 

    20        nLargest = nIndex; 

    21    } 

    22  

    23    if (nR <= nHeapSize && Ary[nLargest] < Ary[nR]) 

    24    { 

    25        nLargest = nR; 

    26    } 

    27  

    28    if (nLargest != nIndex) 

    29    { 

    30        // 调整后可能仍然违反堆性质 

    31        Swap(Ary[nLargest], Ary[nIndex]); 

    32        MaxHeapify(Ary, nLargest, nHeapSize); 

    33    } 

    34}

由于一次调整后，堆仍然违反堆性质，所以需要递归的测试，使得整个堆都满足堆性质

MaxHeapify(A,1,9)作用过程如图所示

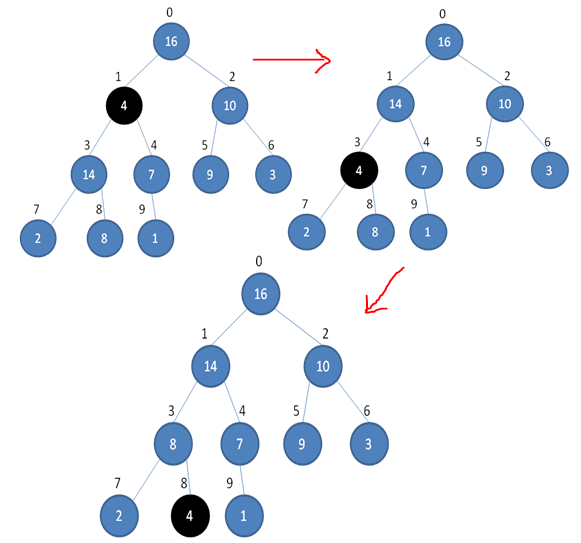
对于有n个元素的堆来说，MaxHeapify的运行时间最坏情况是O(logn)（可以通过主定理的得到）。而在事实上，这个复杂度和堆的高度成正比。我们可以证明，一个大小为n的最大堆，他的高度是lowerbound(logn)

$gif.latex?%5C150dpi%20Suppose~the~height~of~Max~Heap~is~h%5C%5C%20%5Cindent%20So,~we~can~easily~draw~a~conclusion%5C%5C%20%5Cindent%20Maxinum~of~the~elements~is~%5Csum_%7Bk=0%7D%5E%7Bh%7D2%5E%7Bk%7D=2%5E%7Bh+1%7D-1%5C%5C%20%5Cindent%20Mininum~of~the~elements~is~%5Csum_%7Bk=0%7D%5E%7Bh-1%7D2%5E%7Bk%7D+1=2%5E%7Bh%7D%5C%5C%20%5Cindent%20obviously,~2%5E%7Bh%7D%5Cleq%20n%5Cleq%202%5E%7Bh+1%7D-1<%202%5E%7Bh+1%7D%5CRightarrow%20%5C%5C%20%5Cindent%20h%20%5Cleq%20logn<h+1%5CLeftrightarrow%20h=%5Cleft%20%5Clfloor%20logn%20%5Cright%20%5Crfloor$

MaxHeapify很简洁漂亮，但是由于递归的调用可能是某些编译器产生“比较烂”的代码。

通常来说，递归主要用在分治法中，而这里并不需要分治。而且递归调用需要压栈/清栈，和迭代相比，性能上有略微的劣势。当然，按照20/80法则，这是可以忽略的。但是如果你觉得用递归会让自己心里过不去的话，也可以用迭代，比如下面酱紫

 
    01/* 

    02    输  入: Ary(int[]) - [in,out]排序数组 

    03            nIndex(int) - 起始下标 

    04            nHeapSize(int) - 堆大小 

    05    输  出: - 

    06    功  能: 从nIndex开始检查并保持最大堆性质 

    07*/

    08void MaxHeapify(int Ary[], int nIndex, int nHeapSize) 

    09{ 

    10    while(true) 

    11    { 

    12        int nL = LEFT(nIndex); 

    13        int nR = RIGHT(nIndex); 

    14        int nLargest; 

    15  

    16        if (nL <= nHeapSize && Ary[nIndex] < Ary[nL]) 

    17        { 

    18            nLargest = nL; 

    19        } 

    20        else

    21        { 

    22            nLargest = nIndex; 

    23        } 

    24  

    25        if (nR <= nHeapSize && Ary[nLargest] < Ary[nR]) 

    26        { 

    27            nLargest = nR; 

    28        } 

    29  

    30        if (nLargest != nIndex) 

    31        { 

    32            // 调整后可能仍然违反堆性质 

    33            Swap(Ary[nLargest], Ary[nIndex]); 

    34            nIndex = nLargest; 

    35        } 

    36        else

    37        { 

    38            break; 

    39        } 

    40    } 

    41}

显然没有上个版本的漂亮- -

2.2BuildMaxHeap

BuildMaxHeap的作用是将一个数组改造成一个最大堆，接受数组和堆大小两个参数

BuildMaxHeap中自下而上的调用MaxHeapify来改造数组，建立最大堆。因为MaxHeapify能够保证下标i的结点之后结点都满足最大堆的性质，所以自下而上的调用MaxHeapify能够在改造过程中保持这一性质。

如果最大堆的数量元素是n，那么BuildMaxHeap从PARENT(n)开始，往上依次调用MaxHeapify。

这基于一个定理：如果最大堆有n个元素，那么从PARENT(n)+1，PARENT(n)+2…n都是叶子结点（叶子结点指没有儿子结点的结点）

BuildMaxHeap的代码如下：

 
    01/* 

    02    输  入: Ary(int[]) - [in,out]排序数组 

    03            nHeapSize(int) - [in]堆大小(zero-based) 

    04    输  出: - 

    05    功  能: 将一个数组改造为最大堆 

    06*/

    07void BuildMaxHeap(int Ary[], int nHeapSize) 

    08{ 

    09    for (int i = PARENT(nHeapSize); i >= 0; --i) 

    10    { 

    11        MaxHeapify(Ary, i, nHeapSize); 

    12    } 

    13}

由于MaxHeapify的最坏情况是O(logn)，所以BuildMaxHeap的最坏情况是O(nlogn)，虽然这个复杂度是正确的（O给出复杂度的上界），但是不够精确。

事实上，可以利用数学分析证明，BuildMaxHeap的期望复杂度是O(n)

而且，如果对一个递减排列的数组来说，MaxHeapify的复杂度是O(1)，BuildMaxHeap的复杂度也达到最优的O(n)，cos一个递减排列的数组本身满足最大堆

2.3HeapSort

HeapSort是堆排序的接口算法，接受数组和元素个数两个参数

HeapSort先调用BuildMaxHeap将数组改造为最大堆，然后将堆顶和堆底元素交换，之后将底部上升，最后重新调用MaxHeapify保持最大堆性质。

由于堆顶元素必然是堆中最大的元素，所以一次操作之后，堆中存在的最大元素被分离出堆

重复n-1次之后，数组排列完毕。代码如下

 
    01/* 

    02    输  入: Ary(int[]) - [in,out]排序数组 

    03            nCount(int) - [in]元素个数 

    04    输  出: - 

    05    功  能: 对一个数组进行堆排序 

    06*/

    07void HeapSort(int Ary[], int nCount) 

    08{ 

    09    int nHeapSize = nCount - 1; 

    10  

    11    BuildMaxHeap(Ary, nHeapSize); 

    12  

    13    for (int i = nHeapSize; i >= 1; --i) 

    14    { 

    15        Swap(Ary[0], Ary[i]); 

    16        --nHeapSize; 

    17        MaxHeapify(Ary, 0, nHeapSize); 

    18    } 

    19}

排序的过程如图所示

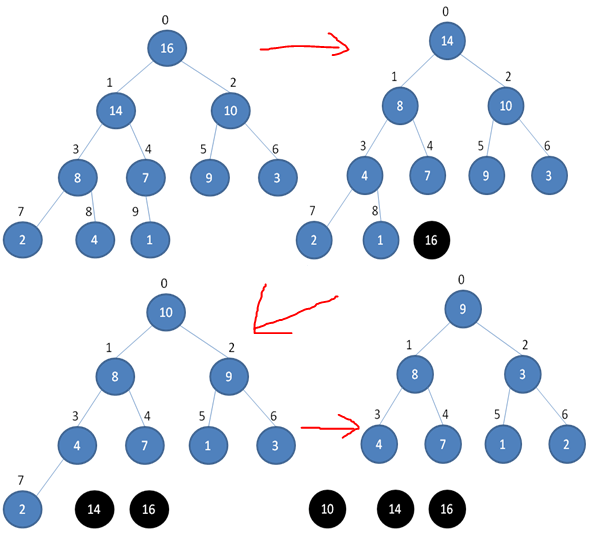
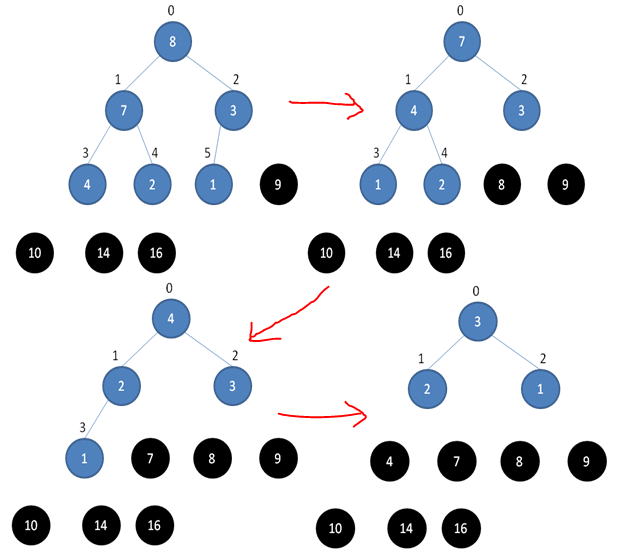
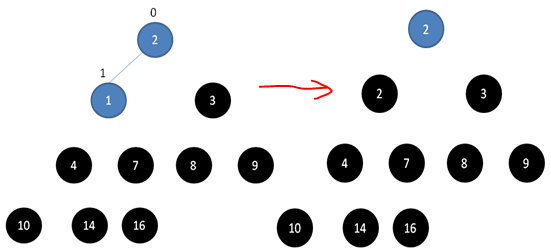
虽然BuildMaxHeap对于不同的初始数据排列所需要的时间不同，但是这并不影响HeapSort的总体时间复杂度

堆作为数据结构，除了用于堆排序之外，更常见的用途是建立优先级队列。

由于最大/最小元素出现在堆根本，所以很容易确定队列元素的优先级。这也是堆最频繁的用途

自http://blog.kingsamchen.com/archives/547#viewSource

转载于:https://www.cnblogs.com/spirals/archive/2010/09/14/1825516.html