基于ANN的6种调制信号自动调制识别（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）

目的： 实现6种（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）调制信号自动调制识别。

 

条件：windows 10，MATLAB 2014a

 

内容： 本实验设计了一个分层结构的MLP神经网络分类器。该分类器使用BP算法，自适应改变判决门限，6种调制信号的整体平均识别率为96.94。

 

更多内容查看：word版（内附完整源代码）下载地址：http://download.youkuaiyun.com/download/lanluyug/9923631

 

一、数字通信调制信号matlab实现原理

1.1二进制振幅键控（2ASK）

振幅键控，就是根据基带信号改变载波的幅度。最简单的实现方式是载波的频率不变，使用二进制信号“0”和“1”控制。2ASK信号可以表示成一个单极性矩形脉冲序列与一个正弦波相乘，其时域表达式为:

 

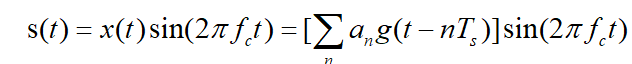
其中matlab代码实现2ASK为：

% 2ASK signal

x=randint(1,M);               %M为64，x为随机生成的1*64的随机矩阵（矩阵元素由0和1组成）

m=sin(2*pi*fc*t);    %载波信号

y=ones(1,M*N);               %M=64,N=200,y为1*12800的全1矩阵

for i=1:M

    for j=1:N

       y((i-1)*N+j)=x(i)*m(j);        %随机生成的2ASK信号

    end

end

 

原理：使用randint()函数生成1*M的随机矩阵（此矩阵由0和1两种元素组成）；此时矩阵x=randint()可充当单极性矩形脉冲序列，最后两层嵌套循环生成2ASK信号：y((i-1)*N+j)=x(i)*m(j);

1.2二进制频移键控（2FSK）

频移键控，就是根据基带信号改变载波的频率。二进制频移键控，是指调制信号“0”和“1”分别对应载波的两个频率f₁和f₂。此时2FSK信号可以看成调整幅度为0和1的两个2ASK信号的叠加，其时域表达式为：

 

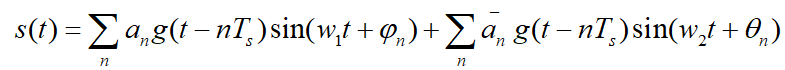
式子中g(t)为单个矩阵脉冲，脉宽为T_s

其中a_n取值如下：

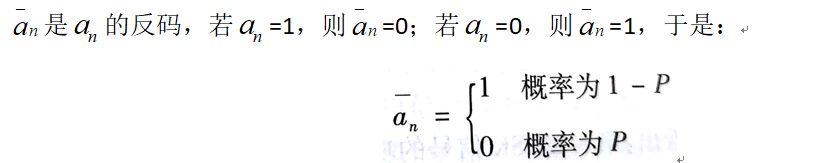
其中matlab代码实现2FSK为：

%2FSK signal

x=randint(1,M); 

m1=sin(2*pi*fc*t);  %载频信号1

m2=sin(2*pi*2*fc*t);      %载频信号2

y=zeros(1,M*N);

for i=1:M         

   if x(i)==1;

    for j=1:N;

        y((i-1)*N+j)=x(i)*m1(j);    %码元信息为1时，为m1频率波形

    end

   elseif  x(i)==0;

     for j=1:N;

       y((i-1)*N+j)=(1-x(i))*m2(j); %码元信息为0时，为m2频率波形

     end

  end

end

原理：使用randint()函数生成1*M的随机矩阵（此矩阵由0和1两种元素组成）；此时矩阵x=randint()可充当单极性矩形脉冲序列，然后两层嵌套for循环加if判断x[i]生成两类2ASK信号，最后叠加成2FSK信号：x[i]=1时，y((i-1)*N+j)=x(i)*m1(j); x[i]=0时，y((i-1)*N+j)=(1-x(i))*m2(j)。

1.3二进制相移键控（2PSK）

二进制相移键控（2PSK）是载波的相位随着二进制数字基带信号而变化，而振幅和频率保持不变。2PSK信号的时域表达式为：

 

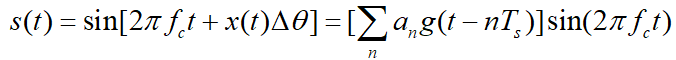
式子中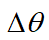是相移常数，式子中是基带序列为“0”和“1”控制。

%2PSK signal,

x=randint(1,M);

m1=sin(2*pi*fc*t);

m2=sin(2*pi*fc*t+pi);

y=zeros(1,M*N);

for i=1:M

   if x(i)==1;

    for j=1:N;

        y((i-1)*N+j)=x(i)*m1(j);

   end

   elseif  x(i)==0;

     for j=1:N;

       y((i-1)*N+j)=(1-x(i))*m2(j);

     end

   end

end

原理：使用randint()函数生成1*M的随机矩阵（此矩阵由0和1两种元素组成）；此时矩阵x=randint()可充当单极性矩形脉冲序列，然后两层嵌套for循环加if判断x[i]生成两类相位相差π的2ASK信号，最后叠加成2PSK信号：当x[i]=1时，m1=sin(2*pi*fc*t); y((i-1)*N+j)=x(i)*m1(j); 当x[i]=0时，m2=sin(2*pi*fc*t+pi);

y((i-1)*N+j)=(1-x(i))*m2(j)。

1.4总结

        4ASK,4FSK,4PSK调制信号matlab代码采用类似手段构成，在此不作介绍，详细信息可以参考最后附录的源代码。再者，本次实验设置参数如下：载波频率fc=20000；采样频率fs=40000；信息码元长度=15*round(k*fs/fc); 信号长度t0=5.5; 采样点个数Ns=256; 符号速率fd=200; 码元个数M=64，信噪比SNR=5dB;更多细节可参考附录源代码，本人在多数代码后面都写有注释。

二、自动调制识别设计与仿真

目前，自动调制识别方法可以分为两大类：统计判决理论方法和统计模式识别方法。本次报告词用后者。

一个通用的模式识别系统由信号预处理、特征提取和分类识别三部分组成。根据识别部分采用不同又可以分为基于决策理论的信号调制识别、基于人工神经网络的信号调制识别和基于支持向量机的信号调制识别。下图为自动调制识别一般流程：

2.1 调制信号特征参数选取

E.E.Azzouz和A.K.Nandi发表多篇调制信号识别的类似文章，利用他们提出的五个参数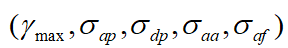，采用判决数的方法对数字信号集（2ASK、4ASK、2FSK、4FSK、2PSK、4PSK）进行识别分类，在信噪比10dB时，识别率高于90%，在信噪比为20dB时，识别率高于96%。