SVM: 相对于logistic regression而言SVM的 cost function与hypothesis

很多学习算法的性能都差不多，关键不是使用哪种学习算法，而是你能得到多少数据量和应用这些学习算法的技巧（如选择什么特征向量，如何选择正则化参数等)

SVM在解决非线性问题上提供了强大的方法。

logistic regression的h(x)

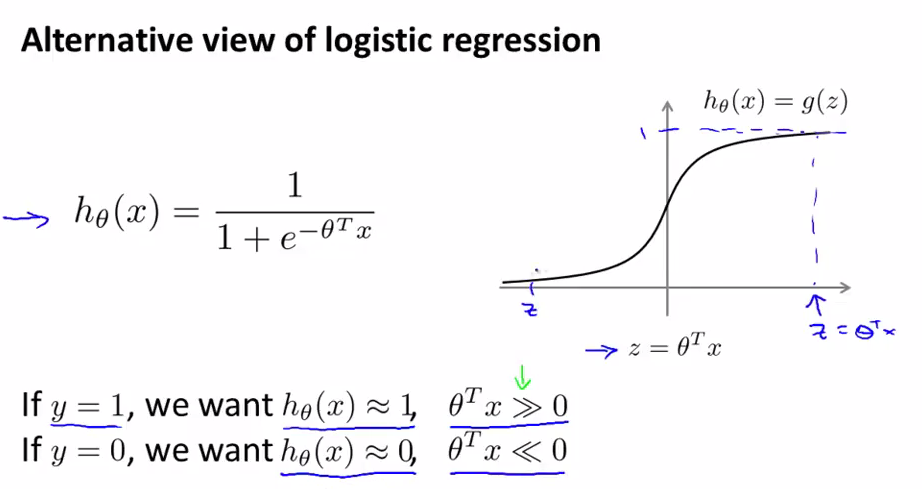
如果y=1,则我们希望h(x)接近于1,即希望θ^Tx要远远大于0

logistic regression的cost function

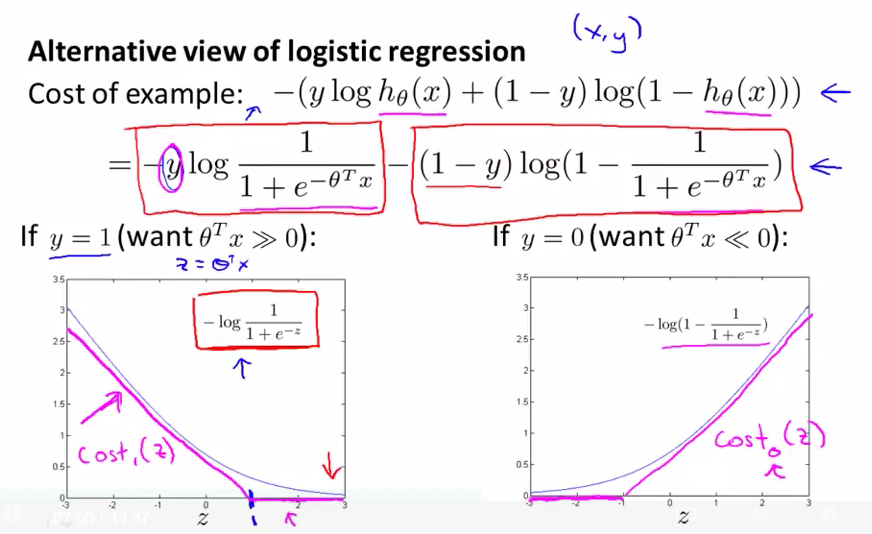
当y=1时的cost function如左图，用粉红色的两段直线近似的代替cost function,记为cost₁(z)(y=1)

当y=0时的cost function如右图，用粉红色的两段直线近似的代替cost function,记为cost₀(z)(y=0)

SVM的cost function

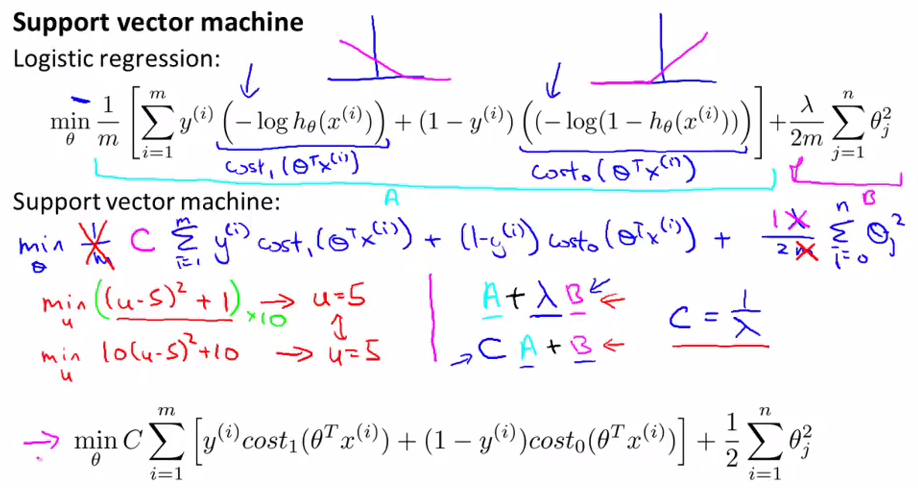
我们用cost₁(z)(y=1)与cost₀(z)(y=0)来代替logistic regression cost function(我们将外面的-移到了里面)中对应的项，然后将1/m去掉（因为cost function整体乘以一个常数求最小值对于取最小值的那个变量来说是不变的）,这样我们用A+λB来表示cost function（A是前面的cost term,B是后面的正则化term）,在SVM中，我们用CA+B来表示cost function（当C=1/λ时，取最小值的θ与logistic regression取最小值时的θ是一至的），这样我们就通过一个变量（C）来对两个term进行权衡（bias 与variance之间的权衡)。

最后，我们得出在SVM中的cost function如最下面的那个式子。

SVM的预测函数(hypothesis)

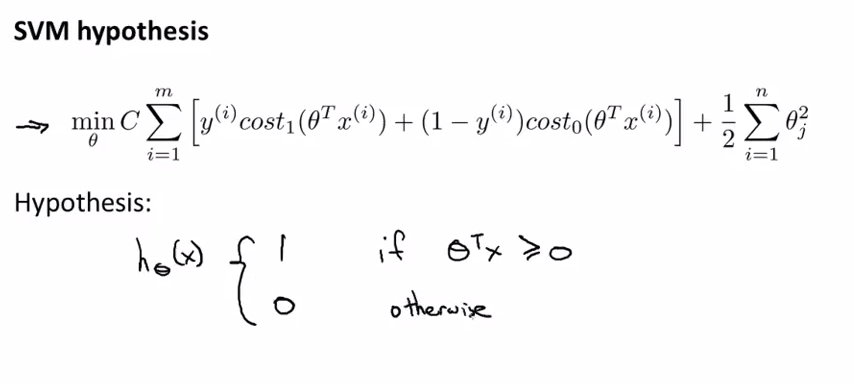
不同于logistic regression用来预测概率（0-1之间）,在SVM中的hypothesis是直接对结果进行预测，如上图所示，当θ^Tx>=0时，hypothesis = 1;

 

转载于:https://www.cnblogs.com/yan2015/p/5176209.html