怎么用计算机求角的度数,如何用转化思想求角的度数？

转化思想是我们数学中常用的一种思想方法。通过对条件的转化，结论的转化使问题化难为易，化未知为已知，最终求出问题的答案。可以说任何一个数学问题都是通过数或形的转化，化归为一个比较熟悉，比较容易的问题，从而达到解决问题的目的。

例：如图，求∠A + ∠B + ∠C + ∠D + ∠E 等于多少度？

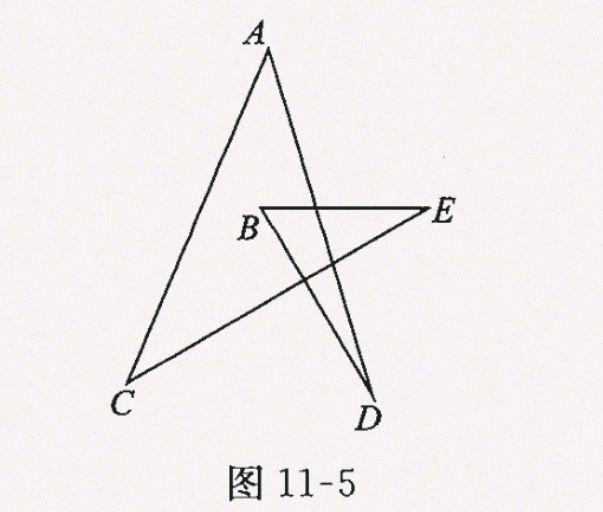
解析：不规则图形内角和的求法，一般是先通过做辅助线。将原图形分割成多个三角形形，再通过三角形外角的性质与所求角建立联系，可能涉及邻补角，对顶角或多边形内角和的应用。

方法一：

解：延长EB交AC于点F,如图

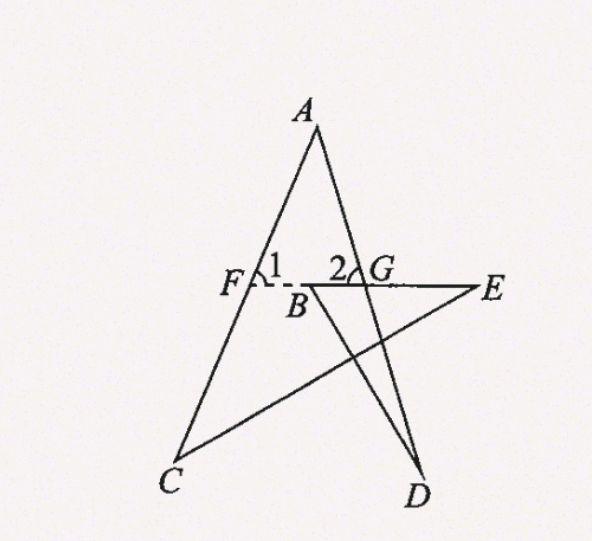
由三角形外角的性质得，

∠1＝∠E＋∠C

∠2＝∠GBD＋∠D

所以∠A + ∠GBD + ∠C + ∠D + ∠E ＝∠A＋∠1＋∠2＝180

方法二：

连接CD，在三角形和三角形COD中

∠BOE＝∠COD

∠OBE＋∠E＝∠OCD＋∠ODC

∠A + ∠B+ ∠ACE + ∠ADB+ ∠E

＝∠A + ∠B+ ∠E＋∠ACE+ ∠ADB

＝∠A + ∠OCD + ∠ODC + ∠ACE＋∠ADB

＝∠A＋∠ACD＋∠ADC＝180

例：已知在三角形ABC中，∠C＞∠B，AD是三角形ABC的一条角平分线

⑴如图①，AE⊥BC于E，试探究∠DAE与∠B，∠C的数量关系

⑵如图②，F是AD上一点，FE⊥BC于E，这时∠DFE与∠B，∠C有怎样的数量关系？请说明理由

⑶如图③，F是线段AD延长线上一点，FE⊥BC于E，这时∠DFE与∠B，∠C有怎样的数量关系？请说明理由

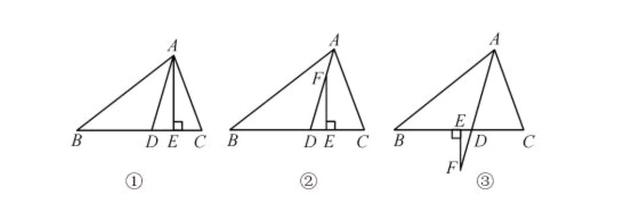
方法一

解：

(1)

∠DAE=90-∠ADE=90-(∠DAB+∠DBA)=90-∠DAB-∠DBA=90-(180-∠B-∠C)/2-∠B=(∠C-∠B)/2

(2)

∠DFE=90-∠ADE=90-(∠DAB+∠DBA)=90-∠DAB-∠DBA=90-(180-∠B-∠C)/2-∠B=(∠C-∠B)/2

(3)

∠DFE=90-∠FDE=90-∠ADC=90-(∠B+∠DAB)=90-∠B-∠DAB=90-∠B-(180-∠B-∠C)/2=(∠C-∠B)/2

方法二

第(1)问如上，

第(2)问，第(3)问，过点A作AG垂直于BC，∠DFE=∠DAG即可求出∠DFE、∠B、∠C之间的关系。

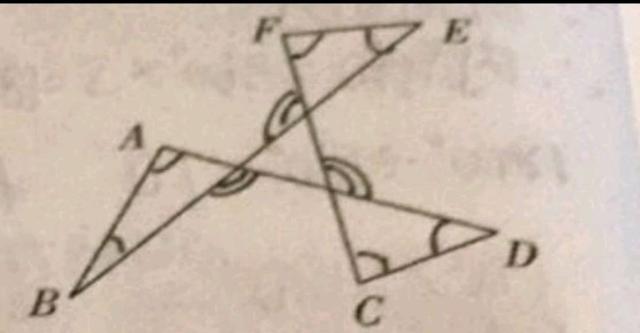
练习：如图，求∠A + ∠B + ∠C + ∠D + ∠E ＋∠F等于多少度？

举报/反馈