（快速幂）Key Set--hdu--5363

最新推荐文章于 2025-09-06 17:51:19 发布

weixin_30546933

最新推荐文章于 2025-09-06 17:51:19 发布

阅读量87

点赞数

CC 4.0 BY-SA版权

文章标签： php

原文链接：http://www.cnblogs.com/YY56/p/4712548.html

本文介绍了快速幂算法的实现方法，并提供了两种不同的C++代码实现方案。该算法主要用于解决形如a^b mod m的问题，通过递归的方式将幂运算转换为乘法运算，大大提高了计算效率。

链接：

http://acm.hdu.edu.cn/showproblem.php?pid=5363

http://acm.hust.edu.cn/vjudge/contest/view.action?cid=86698#problem/C

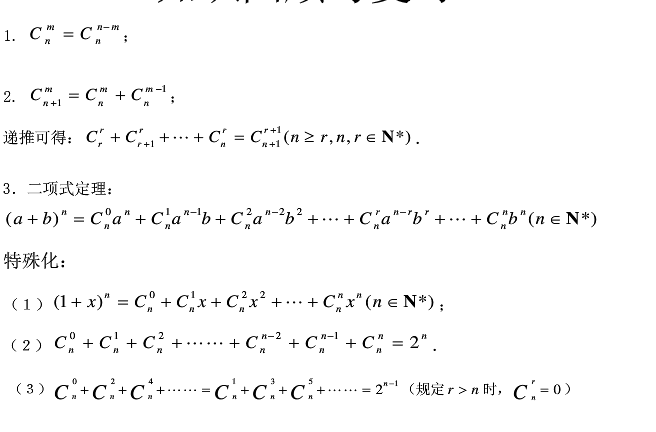
代码：

#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

#define mod 1000000007

long long Pow(long long a, long long b)
{
    if(b==1)
        return a%mod;

      long long  d=Pow(a, b/2);

      if(b%2)
        return d * d * a %mod;
      else
       return d * d % mod;
}

int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        long long n;
        scanf("%lld", &n);

        if(n==1)
        {
            printf("0\n");
            continue;
        }

        long long ans = Pow(2, n-1);

        printf("%lld\n", ans-1);
    }
    return 0;
}

代码2：

#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

#define mod 1000000007


__int64 Pow(int a,int b)
{
    __int64 r=1,base=a;
    while(b)
    {
        if(b&1)
            r=(r*base)%mod;
        base=(base*base)%mod;
        b>>=1;
    }
    return r%mod;
}

int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        long long n;
        scanf("%lld", &n);

        if(n==1)
        {
            printf("0\n");
            continue;
        }

        long long ans = Pow(2, n-1);

        printf("%lld\n", ans-1);
    }
    return 0;
}