有向图的强连通子图&2次DFS

最新推荐文章于 2024-04-07 18:36:03 发布

转载最新推荐文章于 2024-04-07 18:36:03 发布 · 608 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/nzmx123/p/9634238.html

本文介绍了一种求解强连通分量的方法：首先进行一次正常的深度优先搜索（DFS），然后反转所有边的方向，根据第一次DFS的结束时间逆序再次进行DFS。通过这种方法能够有效地找到图中的所有强连通分量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

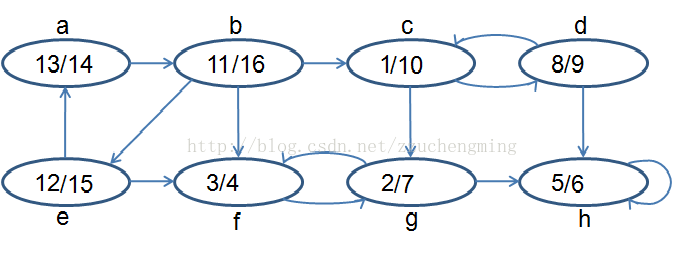
第一次DFS是正常顺序；第二次将edge反向，然后从Finish time最后的点开始DFS。

如下分别是两次DFS。

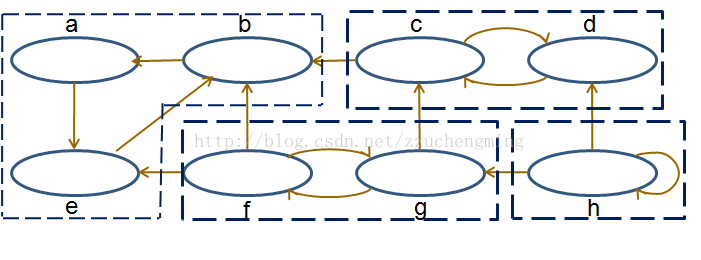
逆序即以b为源节点开始，会得到b->a->e; c->d; g->f; h;四棵子树，即四个强连通分量。

现在解释一下为什么要先反向？

以C结点为例，图未反向时，我们从C能遍历到的结点有，c->g->h->f->d。

图反向后，我们从C能遍历到的结点有，c->d。（注意图反向后，我们是从b开始DFS的）从这里我们可以看出c,d就是一个强连通子图。因为从c的正向出发可以到达d，从反向出发也能到达d，那就说明c，d之间两两都有路径。