算是 PRML第九章的一个笔记。如有错误的地方,欢迎指正。
1. 问题描述
已知随机变量 X 和 Z 具有联合分布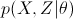 ,其中 X 是可以观测的,Z 是不可观测的(隐变量)。现在给定了 X 的观测值,要求
,其中 X 是可以观测的,Z 是不可观测的(隐变量)。现在给定了 X 的观测值,要求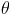 的最大似然估计。即已知 X, 求解优化问题
的最大似然估计。即已知 X, 求解优化问题
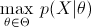
EM算法是在有隐含变量存在时求参数的最大似然估计的一种优化方法。
2. EM算法的推导
假设 Z 是离散型的随机变量(如果 Z 是连续型的随机变量,将下面推导中的求和号换为积分号即可)。记 Z 的取值空间为 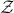 ,设 q(Z) 为 空间
,设 q(Z) 为 空间 ![]() 上的任意一个概率分布函数,则有
上的任意一个概率分布函数,则有
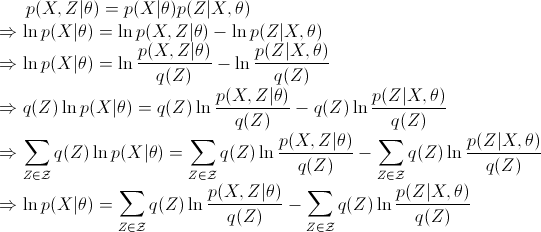
记
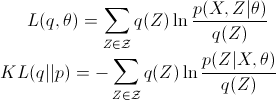
则
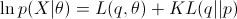
由于相对熵(或称 KL距离) KL(q || p)恒非负,而且满足 KL(q || p) = 0 当且仅当 q 和 p 是同一个分布,所以
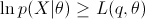
等号成立当且仅当 q ~ Z | X, θ。
有了上述准备,我们可以阐述EM算法的基本流程了。
牢记我们的目标:已知 X , 求使 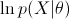 最大的 θ(事实上,EM算法只能找到极大值点)。
最大的 θ(事实上,EM算法只能找到极大值点)。
EM算法的思路是:任意给 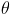 赋一个初值
赋一个初值 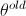 , 然后通过一个迭代过程不断的更新
, 然后通过一个迭代过程不断的更新 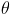 ,每更新一次都保证
,每更新一次都保证 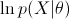 的值在变大,直到不能变大为止(说明已经到了一个极大值点)。
的值在变大,直到不能变大为止(说明已经到了一个极大值点)。
由上面的分析得到,对于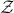 上的任意概率分布 q,恒有
上的任意概率分布 q,恒有
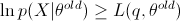
当取 q 为 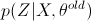 时等号成立,记
时等号成立,记 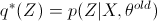 . 则
. 则
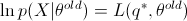
如果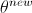 满足
满足 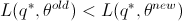 , 则有
, 则有
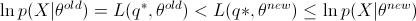
即把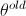 更新为
更新为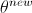 会使得
会使得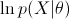 的值增加。
的值增加。
显然
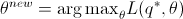
满足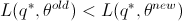 。
。
由于
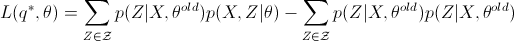
上式中第二项与 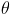 无关,因此
无关,因此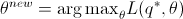 和
和
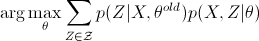
是等价的。
EM算法总结如下:
1. 给定 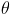 的一个初始值
的一个初始值 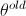 ;
;
2. E-step: 计算 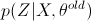 ;
;
3. M-step: 求解优化问题
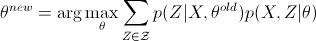
4. 检查是否收敛了,如果没有,则更新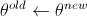 然后回到第 2 步。
然后回到第 2 步。




















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








