Graphcut-1.最大流最小割定理

 

网络流的定义

网络流的三个性质：

 

1、容量限制:  f[u,v]<=c[u,v]
2、反对称性：f[u,v] = - f[v,u]
3、流量平衡:  对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。
只要满足这三个性质,就是一个合法的网络流.

 

最大流问题，就是求在满足网络流性质的情况下，源点 s 到汇点 t 的最大流量。

 

 

一、割的定义

 

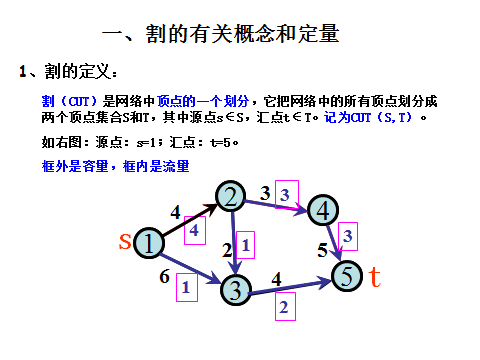
例子：

 

 

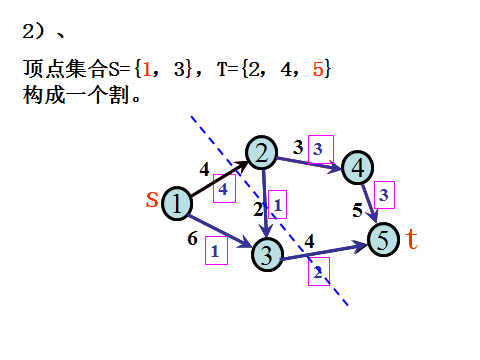
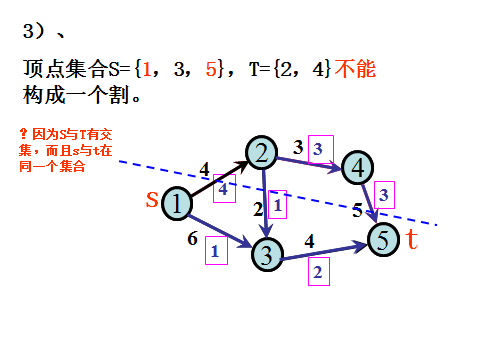
2.割边的概念

 

 

例子：

 

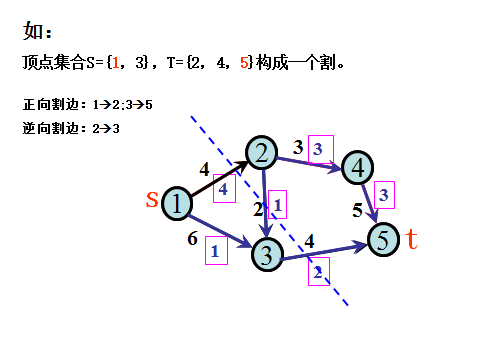
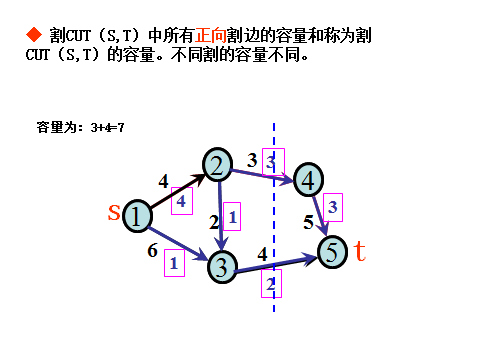
 3.割的容量

 二、网络流与割的关系

 

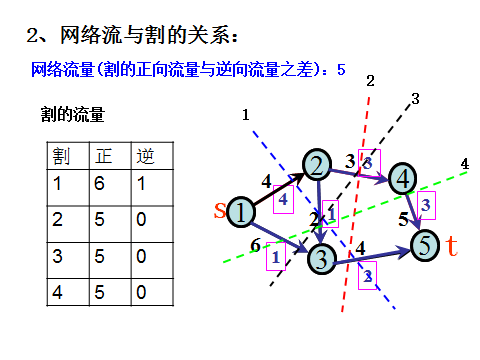
1.结论

 

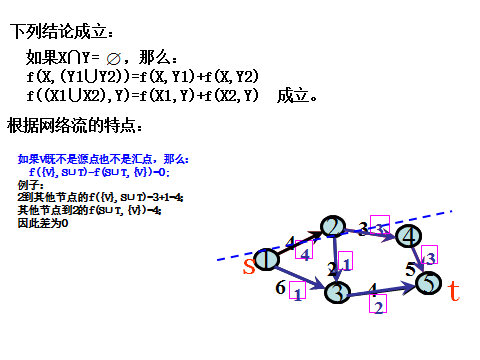
2.定理1:

 

 

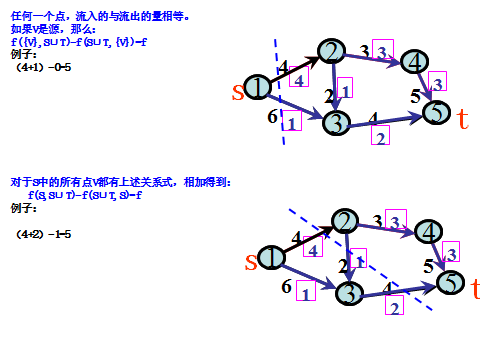
3.推论：

 

4.定理2

 

 5.定理3:

 

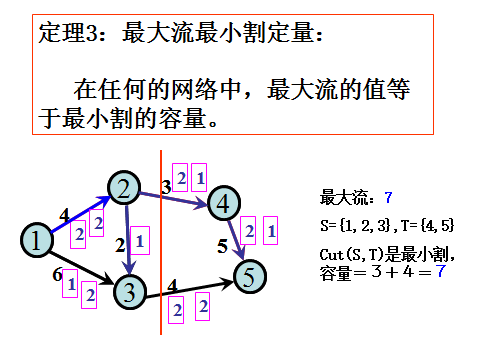
 6.结论：

 7.一些1求解：

 

 

 三、应用实例

 

 

 

 

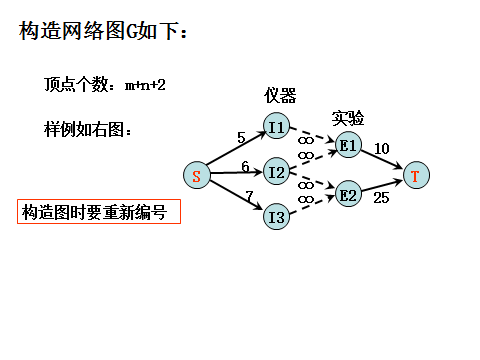
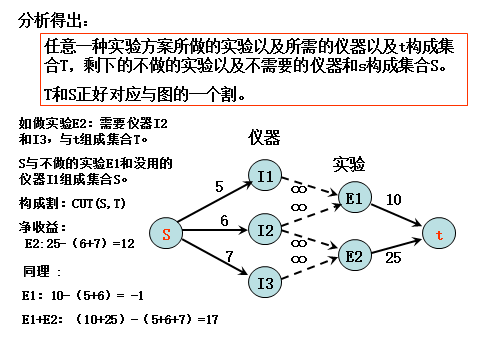
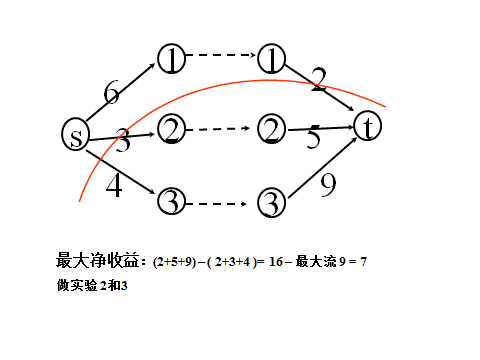
 最大净收益：

 

 

 

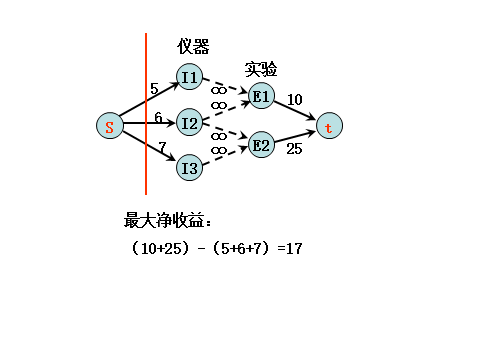
三个实验，三个实验器材：进行实验2与实验3的净收益：

 

至此，最大流与最小割的理论介绍已经结束，感谢有这样一份ppt，基本上能明白其中的原理；这个理论在图割算法中有应用，接下来会继续探究一下。

 

转载于:https://www.cnblogs.com/NarcissusBlog/p/6580281.html