统计计算与随机模拟-优快云博客

计算组合数，choose(n, k)。

计算组合数，choose(n, k)。

生成所有组合，combn(items, k)。

combn(1:5, 3)

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,]    1    1    1    1    1    1    2    2    2     3
## [2,]    2    2    2    3    3    4    3    3    4     4
## [3,]    3    4    5    4    5    5    4    5    5     5

combn(paste0("T", c(1:6)), 3)

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## [1,] "T1" "T1" "T1" "T1" "T1" "T1" "T1" "T1" "T1" "T1"  "T2"  "T2"  "T2" 
## [2,] "T2" "T2" "T2" "T2" "T3" "T3" "T3" "T4" "T4" "T5"  "T3"  "T3"  "T3" 
## [3,] "T3" "T4" "T5" "T6" "T4" "T5" "T6" "T5" "T6" "T6"  "T4"  "T5"  "T6" 
##      [,14] [,15] [,16] [,17] [,18] [,19] [,20]
## [1,] "T2"  "T2"  "T2"  "T3"  "T3"  "T3"  "T4" 
## [2,] "T4"  "T4"  "T5"  "T4"  "T4"  "T5"  "T5" 
## [3,] "T5"  "T6"  "T6"  "T5"  "T6"  "T6"  "T6"

随机数生成。

runif(1)  #0到1上的均匀分布

## [1] 0.3584

rnorm(3, mean = c(-10, 0, 10), sd = 1)  #生成三个随机数，均值不同

## [1] -10.7833  -0.4742   9.6486

rnorm(10, mean = c(-10, 0, 10), sd = 1)  #参数cycle

##  [1] -10.9275   0.6906  10.3180 -10.2367   1.0209   9.2180  -9.1069
##  [8]  -0.6047   9.9559 -10.2503

means <- rnorm(10, mean = 0, sd = 0.2)  #一个层次模型，正态分布的均值来自于标准正态分布
rnorm(10, mean = means, sd = 1)

##  [1]  0.5779587 -0.2777298 -0.6599636  0.0002767 -0.1342494  0.7589831
##  [7]  0.8531856 -0.0085793 -0.3702572  0.5567751

生成可复现的随机数

c(runif(1), runif(1))

## [1] 0.193 0.677

set.seed(666)
c(runif(1), runif(1))

## [1] 0.7744 0.1972

set.seed(666)
c(runif(1), runif(1))

## [1] 0.7744 0.1972

随机抽样函数sample

sample(c("H", "T"), 10, replace = TRUE)  #抽H和T的概率相同

##  [1] "T" "H" "H" "T" "T" "H" "H" "H" "T" "H"

sample(c("H", "T"), 10, replace = TRUE, prob = c(0.2, 0.8))  #自定义抽样概率

##  [1] "T" "T" "T" "H" "T" "H" "T" "T" "H" "T"

sample(1:10)  #随机置换

##  [1]  1  2  7  9 10  4  3  5  6  8

计算概率，d开头是密度函数，p开头是分布函数

dbinom(7, size = 10, prob = 0.5)  #P(X=7)

## [1] 0.1172

pbinom(7, size = 10, prob = 0.5)  #P(X<=7)

## [1] 0.9453

diff(pbinom(c(3, 7), size = 10, prob = 0.5))  #P(3<X<=7)，diff右减左

## [1] 0.7734

计算分位数，q开头的函数

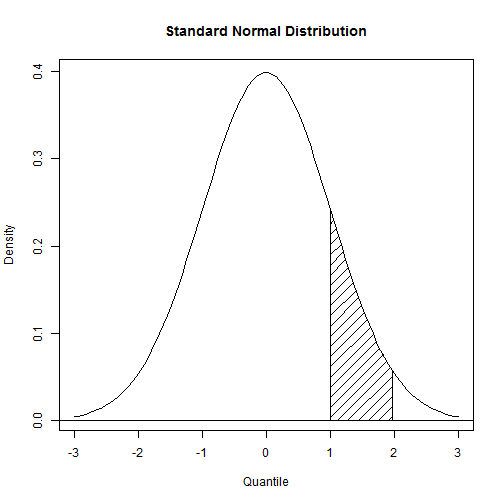
画密度函数

x <- seq(from = -3, to = 3, length.out = 100)
y <- dnorm(x)
region.x <- x[1 <= x & x <= 2]
region.y <- y[1 <= x & x <= 2]
region.x <- c(region.x[1], region.x, tail(region.x, 1))  #函数tail返回region.x的最后一个元素
region.y <- c(0, region.y, 0)
plot(x, y, main = "Standard Normal Distribution", type = "l", ylab = "Density", 
    xlab = "Quantile")
abline(h = 0)
polygon(region.x, region.y, density = 10)  #以45度的斜线填充

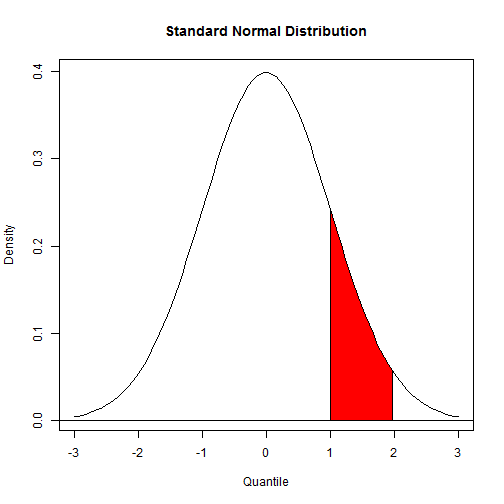
plot of chunk unnamed-chunk-6

plot(x, y, main = "Standard Normal Distribution", type = "l", ylab = "Density", 
    xlab = "Quantile")
abline(h = 0)
polygon(region.x, region.y, density = -1, col = "red")  #填充颜色

plot of chunk unnamed-chunk-6