排序

排序

算法分类

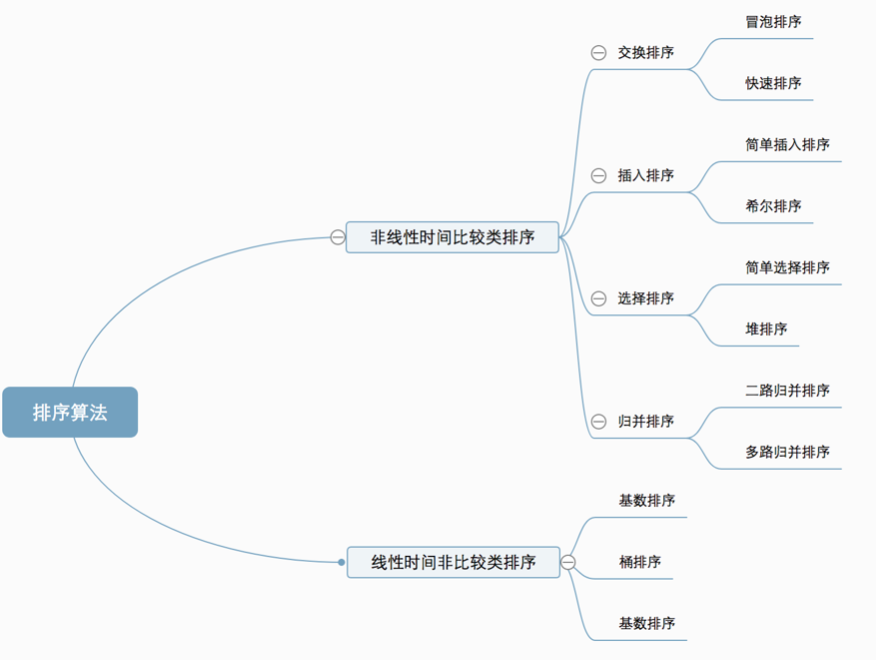
十种常见排序算法可以分为两大类：

非线性时间比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此称为非线性时间比较类排序。

线性时间非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。 

算法复杂度

 

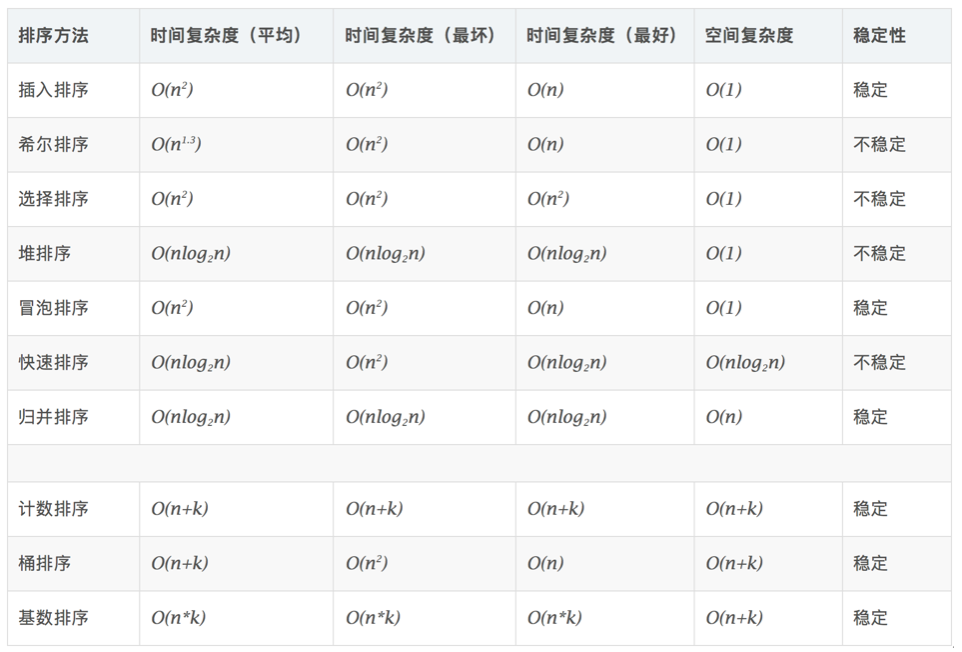
具体算法描述参考博文：

 https://www.cnblogs.com/onepixel/articles/7674659.html

 

题目描述

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

 

方法一：蒂姆排序

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         if tinput = = [] or k > len (tinput):

             return []

         tinput.sort()

         return tinput[: k]

 

方法二：快速排序

思想：每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         def quick_sort(lst):

             if not lst:

                 return []

             pivot = lst[ 0 ]   #基准点

             left = quick_sort([x for x in lst[ 1 : ] if x < pivot])

             right = quick_sort([x for x in lst[ 1 : ] if x > = pivot])

             return left + [pivot] + right

 

         if tinput = = [] or k > len (tinput):

             return []

         tinput = quick_sort(tinput)

         return tinput[: k]

 

方法三：归并排序

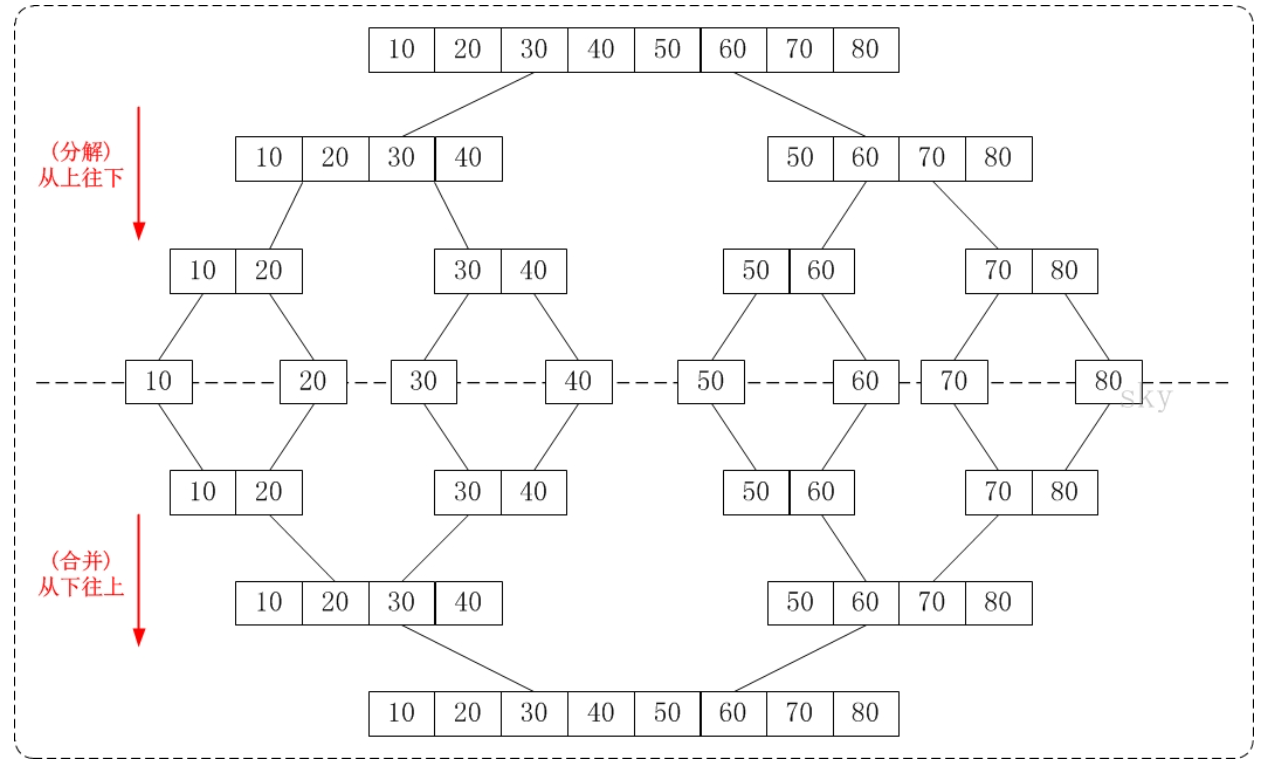
思想：将两个的有序数列合并成一个有序数列，我们称之为" 归并"。 将一个数组一直对半分，问题的规模就减小了，再重复进行这个过程，直到元素的个数为一个时，一个元素就相当于是排好顺序的。接下来就是合并的过程了。一开始合成两个元素，然后合并4个，8个这样进行。

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         def merge_sort(lst):

             if len (lst) < = 1 :

                 return lst

             mid = len (lst) / / 2

             left = merge_sort(lst[: mid])

             right = merge_sort(lst[mid:])

             return merge(left, right)

         def merge(left, right):

             l, r, res = 0 , 0 , []

             while l < len (left) and r < len (right):

                 if left[l] < = right[r]:

                     res.append(left[l])

                     l + = 1

                 else :

                     res.append(right[r])

                     r + = 1

             res + = left[l:]

             res + = right[r:]

             return res

         if tinput = = [] or k > len (tinput):

             return []

         tinput = merge_sort(tinput)

         return tinput[: k]

 

 方法四：堆排序

（这篇文章堆排序写的很详细：https://www.jianshu.com/p/d174f1862601）

设当前元素在数组中以R[i]表示，那么，(1) 它的左孩子结点是：R[2*i+1];  (2) 它的右孩子结点是：R[2*i+2];  (3) 它的父结点是：R[(i-1)/2];

可归纳为两个操作：

（1）根据初始数组去构造初始堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大（最大堆））。

（2）每次交换第一个和最后一个元素，输出最后一个元素（最大值），然后把剩下元素重新调整为大根堆。 

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         def siftup(lst, temp, begin, end):

             if lst = = []:

                 return []

             i, j = begin, begin * 2 + 1

             while j < end:

                 if j + 1 < end and lst[j + 1 ] > lst[j]:

                     j + = 1

                 elif temp > lst[j]:

                     break

                 else :

                     lst[i] = lst[j]

                     i, j = j, 2 * j + 1

             lst[i] = temp

 

         def heap_sort(lst):

             if lst = = []:

                 return []

             end = len (lst)

             for i in range ((end / / 2 ) - 1 , - 1 , - 1 ):

                 siftup(lst, lst[i], i, end)

             for i in range (end - 1 , 0 , - 1 ):

                 temp = lst[i]

                 lst[i] = lst[ 0 ]

                 siftup(lst, temp, 0 , i)

             return lst

 

         if tinput = = [] or k > len (tinput):

             return []

         tinput = heap_sort(tinput)

         return tinput[: k]

 

方法五：冒泡排序

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         def bubble_sort(lst):

             if lst = = []:

                 return []

             for i in range ( len (lst)):

                 for j in range ( 1 , len (lst) - i):

                     if lst[j - 1 ] > lst[j]:

                         lst[j - 1 ], lst[j] = lst[j], lst[j - 1 ]

             return lst

 

         if tinput = = [] or k > len (tinput):

             return []

         tinput = bubble_sort(tinput)

         return tinput[: k]

 

方法六：直接选择排序

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 

 

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         def select_sort(lst):

             if lst = = []:

                 return []

             for i in range ( len (lst) - 1 ):

                 smallest = i

                 for j in range (i, len (lst)):

                     if lst[j] < lst[smallest]:

                         smallest = j

                 lst[i], lst[smallest] = lst[smallest], lst[i]

 

             return lst

 

         if tinput = = [] or k > len (tinput):

             return []

         tinput = select_sort(tinput)

         return tinput[: k]

 

方法七：插入排序

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

 

class Solution:

     def GetLeastNumbers_Solution( self , tinput, k):

         # write code here

         def Insert_sort(lst):

             if lst = = []:

                 return []

             for i in range ( 1 , len (lst)):

                 temp = lst[i]

                 j = i

                 while j > 0 and temp < lst[j - 1 ]:

                     lst[j] = lst[j - 1 ]

                     j - = 1

                 lst[j] = temp

             return lst

 

         if tinput = = [] or k > len (tinput):

             return []

         tinput = Insert_sort(tinput)

         return tinput[: k]

 

posted on 2019-03-04 11:49 竹径风声 阅读( ...) 评论( ...) 编辑 收藏

转载于:https://www.cnblogs.com/girl1314/p/10469843.html