机器学习真的可以起作用吗？（3）（以二维PLA为例）

前两篇文章已经完成了大部分的工作，这篇文章主要是讲VC bound和 VC dimension这两个概念。

（一）前文的一点补充

根据前面的讨论，我们似乎只需要用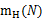来替代来源的M就可以了，但是实际公式却不是这样的，我们需要数学上处理几个小细节。具体的处理方法不讲，只提供大体思路。

可以看出，真实情况下，公式中多了3个参数。

这三个参数是怎么来的？

（1）我们无法计算Eout，所以我们另外采样N个数据，用它来计算E'in，代替Eout，这对于固定的一个h是可行的。

 

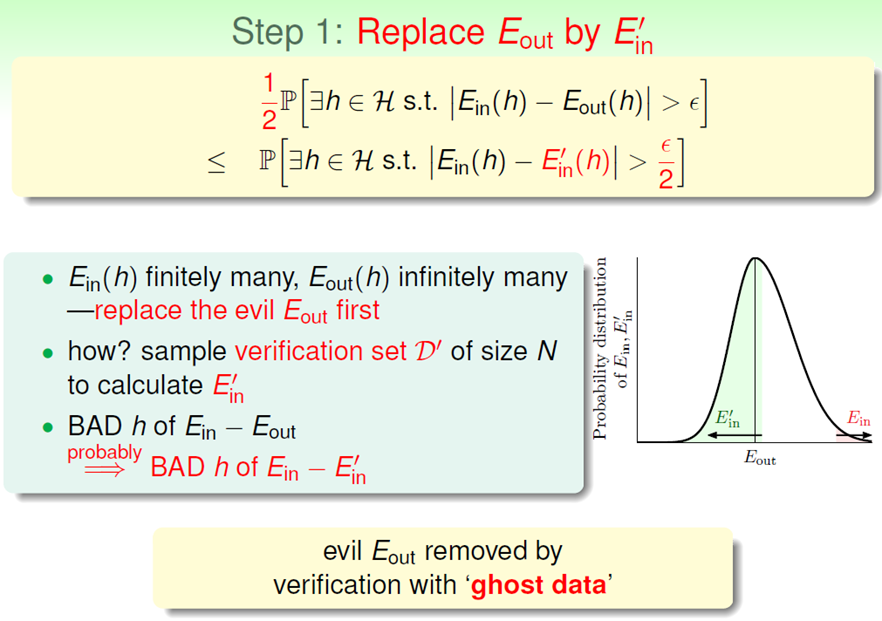
（2）现在我们就变成了取2N个点了

（3）使用Hoffding定理

（4）最终结论称之为VC bound

 

注意：整个证明过程中没有具体到PLA算法，也即这个过程对所有的机器学习算法都适用。

（二）VC Dimension

定义breakpoint –1 为VC dimension。表示为d_vc

可以证明对于PLA算法：d_vc(H)=d+1  (d为w的维度)。

其物理意义是是自由度。这一点非常重要，让我们可以直观地认识一个hypothesis set的d_vc 。

（三）VC bound的两种解释。

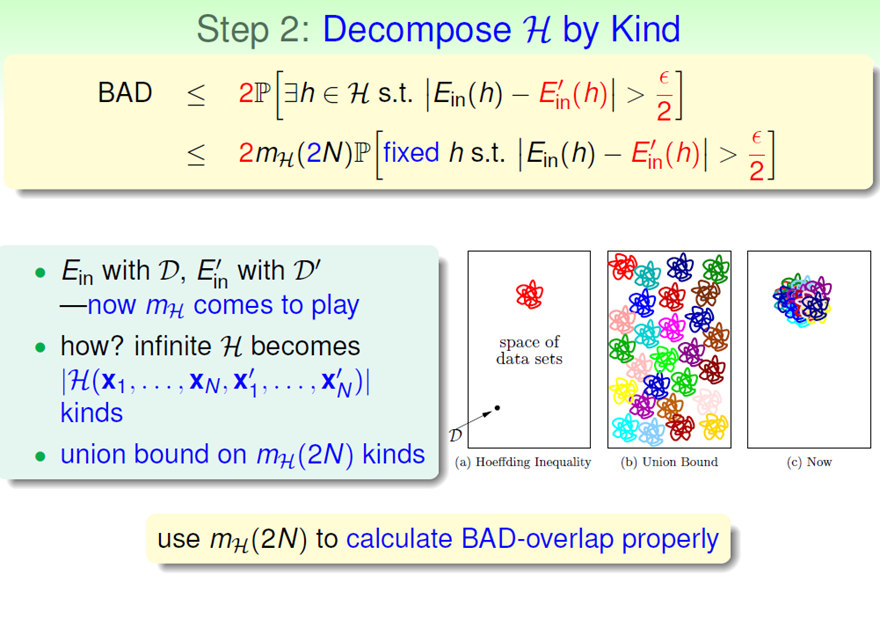
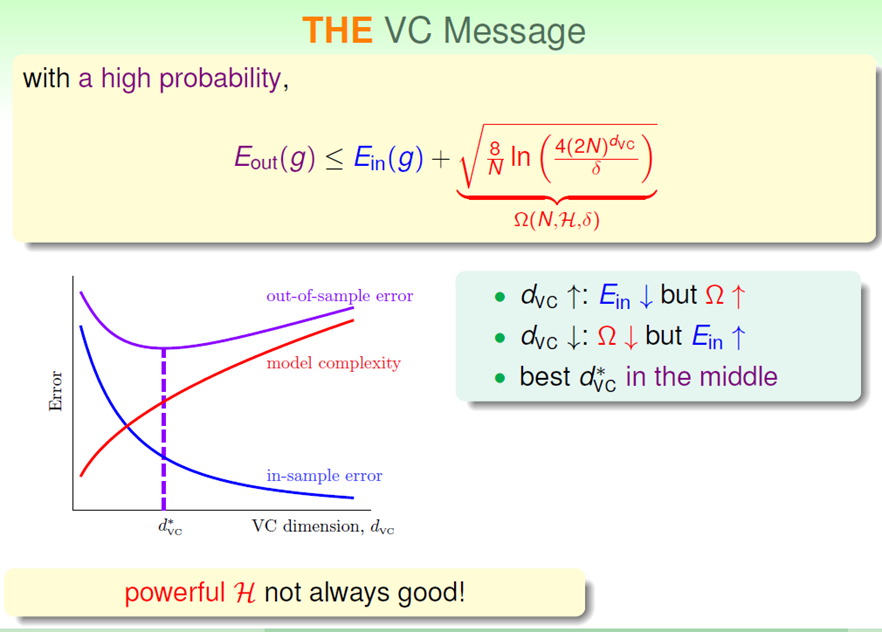
（1）Penalty for Model Complexity

根据上述的关系，可以得出如下结论：

这里的一个重要结论是：一般情况下，最好的选择一般不会出现在Ein最小的地方。

（2）Sample Complexity。

dvc可以提供给我们关于D大小的信息。

可以看出，当δ，ε，d_vc确定的时候，我们就基本可以确定样本量N的大小。

为什么理论上N≈10000d_vc，实际上通常使用10d_vc呢？因为我们得到的这个理论值非常宽松！为什么这么宽松呢？四条理由。

转载于:https://www.cnblogs.com/wangyanphp/p/5438805.html