zkw线段树学习笔记

最新推荐文章于 2024-03-24 18:24:03 发布

weixin_30492047

最新推荐文章于 2024-03-24 18:24:03 发布

阅读量109

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/spaceskynet/p/6550942.html

PS:

说起线段树，可谓是一把辛酸泪（尽管我喜欢打树状数组？?）。代码较长？（似乎是滴）,TLE（屡见不鲜）,递归建树（!!!）,说实在，不得不用（说到底lowbit差了些，你懂的）。

先来一发线段树：

#include<iostream>
#include<cstdio>
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
const int maxn=2e4;
int segtree[maxn*4+10],array[maxn];
void build(int,int,int);
int query(int,int,int,int,int);
void updata(int,int,int,int,int);
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&array[i]);
	}
	build(1,1,n);
	……………………
	return 0;
}
void build(int node,int begin,int end)//node结点，begin为array某子区间首标号，end为某子区间末标号。
{
	if(begin==end)
	{
		segtree[node]=array[begin];//首末相等，直接赋值。
	}
	else
	{
		build(2*node,begin,(begin+end)>>1);//区间长度不为一，左右递归。
		build(2*node,(begin+end)>>1+1,end);
		/*---------------区间min------------*/
		if(segtree[2*node]<=segtree[2*node+1])//max改为?>=?
		{
			segtree[node]=segtree[2*node];
		}
		else
		{
			segtree[node]=segtree[2*node+1];
		}
		/*-------------------------------*/
		
		/*---------------区间和------------*/
		segtree[node]=(segtree[2*node]+segtree[2*node+1]);
		/*---------------------------*/
	}
}
int query(int node,int begin,int end,int left,int right)
{
	int p1,p2;
	if(left>end||right<begin)
	{
		return -1;
	}
	if(left<=end&&right>=begin)
	{
		return segtree[node];
	}
	p1=query(2*node,begin,(begin+end)>>1,left,right);
	p2=query(2*node+1,(begin+end)>>1+1,end,left,right);
	if(p1==-1)
	{
		return p2;
	}
	if(p2==-1)
	{
		return p1;
	}
	if(p1<=p2)
	{
		return p1;
	}
	else
	{
		return p2;
	}
}
void updata(int node,int begin,int end,int pos,int val)
{
	if(begin==end)
	{
		segtree[node]+=val;
		return;
	}
	int m=(left+right)>>1+1;
	if(pos<=m)
		updata(2*node,begin,(begin+end)>>1,pos,val);
	else
		updata(2*node+1,(begin+end)>>1+1,end,pos,val);
	/*----MIN--*/
	segtree[node]=min(segtree[2*node],segtree[2*node+1]);
	/*---------*/
}

真长（还没写完）！！！

当我在不久前，看到了zkw（不要误会），我的世界豁然开朗，代码王者荣耀归来，多年守望简洁先锋，终于get到zkw神器。（实际上我只玩MC）

zkw（张昆玮大神）:男，身处清华大学。zkw线段树出自《统计的力量》。

Total:

zkw线段树

1.建树非常简单。

2.线段树能干的，它都行。（似乎是这样的）

3.更多惊喜等你来发掘……

Step1(建树):

首先，堆式储存是关键。——《统计的力量》

堆想必不用多说,用堆是zkw（重口味）的一大特点,如下图：

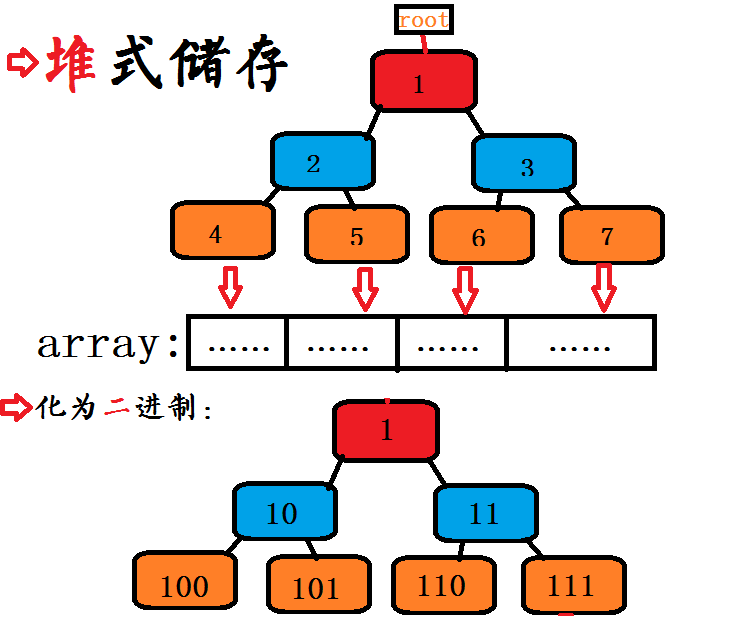
一、化为二进制后不难看出，叶子节点的父节点是它的前缀。———>>也就是说，找父亲只需右移一位（>>）!

二、相反，找父节点的叶子就左移————>>左移一位为左儿子，再+1（或者|1）为右儿子。

三、第n层节点个数为2^(n-1)。

四、Last but not least，最底层节点个数为你实际最多可以操作的数的个数（换个说法，应该可以叫做值域，为2的次幂）。！！！（最重要）

有了它们，就可以开始踏上理论化为现实的伟大道路。

实践开始！

实际上，很多时候数组中数都不是2的次幂，怎么办？————>>直接开2的次幂就行了，多的空间不要了。

————《统计的力量》

一、我们知道，最底层实际上存的是原数组，同时由于堆式储存的特性，序号也是顺序排列的，也就是说————>>当我们需要查询或修改时，只需在原数组序号上加上一个数，设为m吧。

如何求m？

for(m=1;m<n;m<<=1);

实际上，m为最底层所有节点的父节点总数，所以只需设m为1，不断左移，当m>=n时停止。

对于叶子直接输入，对于父节点从叶子（继承？区间和,最大值,最小值……）。

build函数轻松得出：

void build(int n)
{
	for(m=1;m<n;m<<=1);
	//m<<=1;//避免查端点值出错
	for(int i=m+1;i<n+m+1;i++) scanf("%d",&a[i]);//从m+1叶子节点开始，避免查询[1,...]时出错。
	for(int i=m-1;i;--i) a[i]=a[i<<1]+a[i<<1|1];//区间和
/*
for(int i=m-1;i;--i) a[i]=max(a[i<<1],a[i<<1|1]);//最大值
for(int i=m-1;i;--i) a[i]=min(a[i<<1],a[i<<1|1]);//最小值
*/
}

Step2(操作):

线段树最经典（也就是我们为何用如此……的线段树）的便是查询修改操作了，时间复杂度比较平均，都为O（logn）。

单点修改

首先说说单点修改。

我们都知道，线段树是由上到下遍历的，而zkw由于可以直接找到叶子，是由下到上遍历的，因此避免了许多多余的访问，对于单点修改，我们只需将需要修改的点找到（加上m），并循环应用到自己、父节点直到根节点，方便了许多。

void updata(int pos,int val)
{
	a[pos+=m]+=val;
	while(pos)
	{
		a[pos>>=1]=a[pos<<1]+a[pos<<1|1];
	}
}

单点查询

单点a[q]？直接查[q,q]不就行了嘛。对，这是没错。但我们要将它变得复杂一些（并不是搞笑，说实在的，谁愿意写长篇大论的code），这是为了RMQ做准备，这是我们需要一个神奇的东西——差分，把子节点所存的值维护为与其父节点的差值。

所以，build函数需要改改：

void build(int n)//区间和
{
	for(;m<n;m<<=1);
	//m<<=1;//避免查端点值出错
	for(int i=m+1;i<n+m+1;i++) scanf("%d",&a[i]);//从m+1叶子节点开始，避免查询[1,...]时出错。
	for(int i=m-1;i;--i) 
	{
		a[i]=min(a[i<<1],a[i<<1|1]);
		a[i<<1]-=a[i],a[i<<1|1]-=a[i];
	}
}

此时的查询，只需从叶子节点不断循环加上父节点直到根节点。

int point(int x)
{
	int ans=0;
    while(x) 
	{
		ans+=a[x],x>>=1;
	}
	return ans;
}

区间查询

查询区间和，暂且设区间为[l,r]吧，zkw又一特点，化为(l-1,r+1)开区间计算。

因此，这就是为何输入时要从m+1开始，避免查询[1,...]时出错，若要查询[0,……]，下标需加上1。

int query(int l,int r)
{
	int ans=0;
	for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1)
	{
		if(~l&1) ans+=a[l^1];
		if(r&1) ans+=a[r^1];
	}
	return ans;
}

~l&1,意思是是否为左儿子，对于兄弟节点来说，最低位为0或1,0为左儿子，1为右儿子，对于左端点 l 来说，我们只需向右合并更新ans（加上兄弟节点，也就是右节点，l^1），而不管其左边。

r&1，同理，意思是是否为右儿子。

每次循环后移向其父节点继续操作，出口为l^r^1,为什么？若l和r不为同一点或兄弟节点，l^r^1一定为true，否则在为同一点或兄弟节点时跳出循环。

求max

将更新时+改为max就行了。

int query(int l,int r)
{
	int ans=0;
	for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1)
	{
		if(~l&1) ans=max(a[l^1],ans);
		if(r&1) ans=max(a[r^1],ans);
	}
	/************
	int mid=max(l,r);
	while(mid)
	{
		ans+=a[mid>>=1];//差分时定要记住回归，不要只将差值max输出
	}
	*************/
	return ans;
}

求min

将上述max改为min。

区间修改

最简单的无非区间加减（但我也只说这个），和区间查询一样，只要将更新ans改为a[i]+=val，加上差分回归（需用差分）。

void intervalup(int l,int r,int val)
{
	int tmp=0;
	for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1)
	{
		if(~l&1) a[l^1]+=val;
		if(r&1) a[r^1]+=val;
		tmp=min(a[l],a[l^1]),a[l]-=tmp,a[l^1]-=tmp,a[l>>1]+=tmp;
		tmp=min(a[r],a[r^1]),a[r]-=tmp,a[r^1]-=tmp,a[r>>1]+=tmp;
	}
	while(l) tmp=min(a[l],a[l^1]),a[l]-=tmp,a[l^1]-=tmp,a[l>>=1]+=tmp;
}

Last:

以上便是zkw的最基本内容，简单也不简单，最后，来一串zkw类。

//powered by:spaceskynet 2017-03-06
const int maxn=1e5;
class zkw
{
public:
	zkw()
	{
		m=1;
	}
	void build(int n)//区间和
	{
		for(;m<n;m<<=1);
		//m<<=1;//避免查端点值出错
		for(int i=m+1;i<n+m+1;i++) scanf("%d",&a[i]);//从m+1叶子节点开始，避免查询[1,...]时出错。
		for(int i=m-1;i;--i) a[i]=a[i<<1]+a[i<<1|1];
		/**差分建树
		for(int i=m-1;i;--i)
		{
			a[i]=min(a[i<<1],a[i<<1|1]);
			a[i<<1]-=a[i],a[i<<1|1]-=a[i];
		}
		**/
	}
	int query(int l,int r)
	{
		int ans=0;
		for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1)
		{
			if(~l&1) ans+=a[l^1];
			if(r&1) ans+=a[r^1];
		}
		/************
		int mid=max(l,r);
		while(mid)
		{
			ans+=a[mid>>=1];//差分时定要记住回归，不要只将差值max输出
		}
		*************/
		return ans;
	}
	void updata(int pos,int val)
	{
		a[pos+=m]+=val;
		while(pos)
		{
			a[pos>>=1]=a[pos<<1]+a[pos<<1|1];
		}
	}
	void intervalup(int l,int r,int val)
	{
		int tmp=0;
		for(l+=m-1,r+=m+1;l^r^1;l>>=1,r>>=1)
		{
			if(~l&1) a[l^1]+=val;
			if(r&1) a[r^1]+=val;
			tmp=min(a[l],a[l^1]),a[l]-=tmp,a[l^1]-=tmp,a[l>>1]+=tmp;
			tmp=min(a[r],a[r^1]),a[r]-=tmp,a[r^1]-=tmp,a[r>>1]+=tmp;
		}
		while(l) tmp=min(a[l],a[l^1]),a[l]-=tmp,a[l^1]-=tmp,a[l>>=1]+=tmp;
	}
	int point(int x)//差分单点查询
	{
		int ans=0;
		while(x) 
		{
			ans+=a[x],x>>=1;
		}
		return ans;
	}
private:
	int a[2*maxn+2],m;
};

转载于:https://www.cnblogs.com/spaceskynet/p/6550942.html