pca 累积方差贡献率公式_R语言 PCA主成分分析

最新推荐文章于 2025-05-29 21:31:25 发布
最新推荐文章于 2025-05-29 21:31:25 发布
阅读量6.5k 收藏 2
点赞数 2
CC 4.0 BY-SA版权
文章标签： pca 累积方差贡献率公式
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_30476025/article/details/112213718
本文介绍了R语言中PCA主成分分析的统计学背景，包括协方差和相关系数的概念，接着通过实例讲解了PCA的过程，如载入数据、主成分分析、结果解读，并展示了如何画主成分的碎石图和散点图。通过分析，前两个主成分的累积方差贡献率达到96.36%，可用于数据降维。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

微信公众号：生信小知识
关注可了解更多的教程及生信知识。问题或建议，请公众号留言;

R语言 PCA主成分分析

前言统计学背景知识协方差相关系数函数总结实例讲解1.载入原始数据2.作主成分分析3.结果解读4.画主成分的碎石图并预测5.PCA结果绘制后记

前言

PCA分析大家肯定经常看到，但是你真的懂PCA分析的结果吗？

图我也会看，我只是不是很清楚PCA背后输出结果的解读而已。正好看到一篇不错的博客，就把主要的知识点记录下 。

reference:

  • http://www.cnblogs.com/longzhongren/p/4300593.html

  • https://www.zhihu.com/question/20852004

  • 223.主成分分析PCA

统计学背景知识

协方差

可以通俗的理解为：两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？

  • 你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的。

  • 你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。

从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。

从公式出发来理解一下：

a86efb828c93b8d5dd450afba1f3875d.png

公式简单翻译一下是：如果有X，Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值(其实是求“期望”，但就不引申太多新概念了，简单认为就是求均值了)。

具体例子可以去知乎详细查看：

https://www.zhihu.com/question/20852004

相关系数

对于相关系数，我们从它的公式入手。一般情况下，相关系数的公式为：

3b086f650481a8b04526bcc485d5129f.png

翻译一下：就是用X、Y的协方差除以X的标准差和Y的标准差。

所以，相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

既然是一种特殊的协方差，那它：

1、也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。

2、由于它是标准化后的协方差，因此更重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。

具体例子可以去知乎详细查看：

https://www.zhihu.com/question/20852004

函数总结

注意：这里的输入数据，rownames是样本名，colnames是样本的特征。(与正常数据正好相反，需要用t()来转置数据)

  • princomp()主成分分析  可以从相关阵或者从协方差阵做主成分分析

  • fviz_pca_ind对princomp()结果进行展示

  • summary()提取主成分信息

  • loadings()显示主成分分析或因子分析中载荷的内容

  • predict()预测主成分的值

  • screeplot()画出主成分的碎石图

  • biplot()画出数据关于主成分的散点图和原坐标在主成分下的方向

实例讲解

现有30名中学生身高、体重、胸围、坐高数据，对身体的四项指标数据做主成分分析。

1.载入原始数据
# 清空环境
rm(list = ls())
options(stringsAsFactors = F)

# 准备数据
if (T) {
  test    X1=c(148, 139, 160, 149, 159, 142, 153, 150, 151, 139,
         140, 161, 158, 140, 137, 152, 149, 145, 160, 156,
         151, 147, 157, 147, 157, 151, 144, 141, 139, 148),
    X2=c(41, 34, 49, 36, 45, 31, 43, 43, 42, 31,
         29, 47, 49, 33, 31, 35, 47, 35, 47, 44,
         42, 38, 39, 30, 48, 36, 36, 30, 32, 38),
    X3=c(72, 71, 77, 67, 80, 66, 76, 77, 77, 68,
         64, 78, 78, 67, 66, 73, 82, 70, 74, 78,
         73, 73, 68, 65, 80, 74, 68, 67, 68, 70),
    X4=c(78, 76, 86, 79, 86, 76, 83, 79, 80, 74,
         74, 84, 83, 77, 73, 79, 79, 77, 87, 85,
         82, 78, 80, 75, 88, 80, 76, 76, 73, 78)
  )
  rownames(test) "student_",1:30)
  colnames(test) "height","weight","chest","sit-h")
}
2.作主成分分析
# PCA分析
if (T) {
  test.prTRUE)
  summary(test.pr,loadings=TRUE)
}

# Importance of components:
#                           Comp.1     Comp.2     Comp.3     Comp.4
# Standard deviation     1.8817805 0.55980636 0.28179594 0.25711844
# Proportion of Variance 0.8852745 0.07834579 0.01985224 0.01652747
# Cumulative Proportion  0.8852745 0.96362029 0.98347253 1.00000000
# 
# Loadings:
#        Comp.1 Comp.2 Comp.3 Comp.4
# height  0.497  0.543  0.450  0.506
# weight  0.515 -0.210  0.462 -0.691
# chest   0.481 -0.725 -0.175  0.461
# sit-h   0.507  0.368 -0.744 -0.232

结果解读：

  • Standard deviation 标准差  其平方为方差=特征值

  • Proportion of Variance 方差贡献率

  • Cumulative Proportion 方差累计贡献率

由结果显示：前两个主成分的累计贡献率已经达到96.36%，可以舍去另外两个主成分，达到降维的目的。

因此可以得到函数表达式：

  • Z1 = 0.497*height + 0.515*weight + 0.481*chest + 0.507*sit-h

  • Z2 = 0.543*height - 0.210*weight - 0.725*chest + 0.368*sit-h

注意要点：

  • princomp()函数中：

cor是逻辑变量，当cor=TRUE表示用样本的相关矩阵R做主成分分析，当cor=FALSE表示用样本的协方差阵S做主成分分析

  • summary()函数中：

loading是逻辑变量，当loading=TRUE时表示显示loading 的内容，loadings的输出结果为载荷是主成分对应于原始变量的系数，即Q矩阵

3.结果解读

这里我们可以看一看得到的test.pr变量的结构：

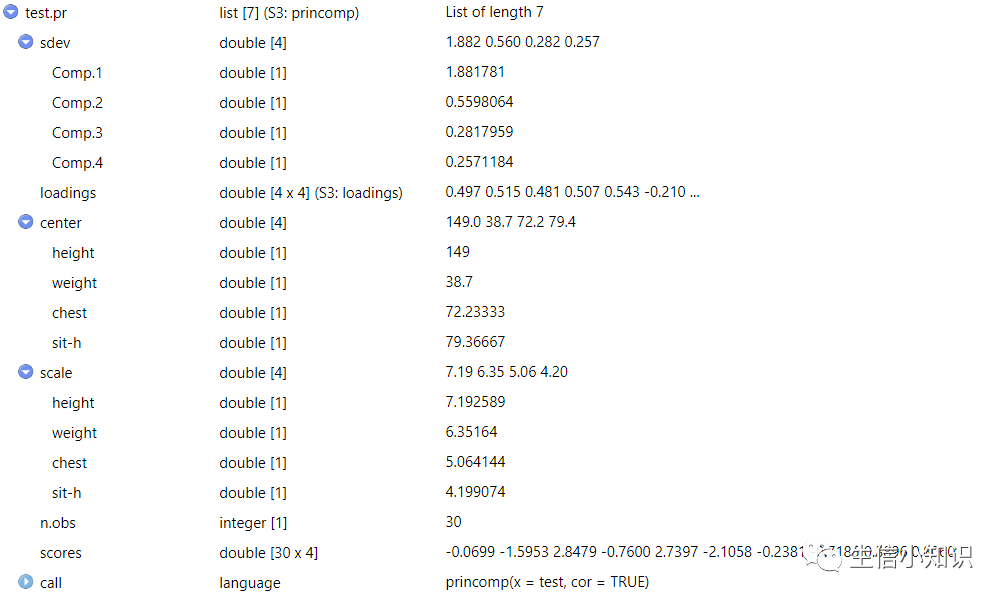
6a8ef3040fc170b46a8bbc3460283d91.png

  • sdev是标准偏差

  • center是每列计算是减去的均值

  • scores即降维之后的结果

我们可以利用函数来验证下scores的结果到底是什么意思：

library(factoextra)
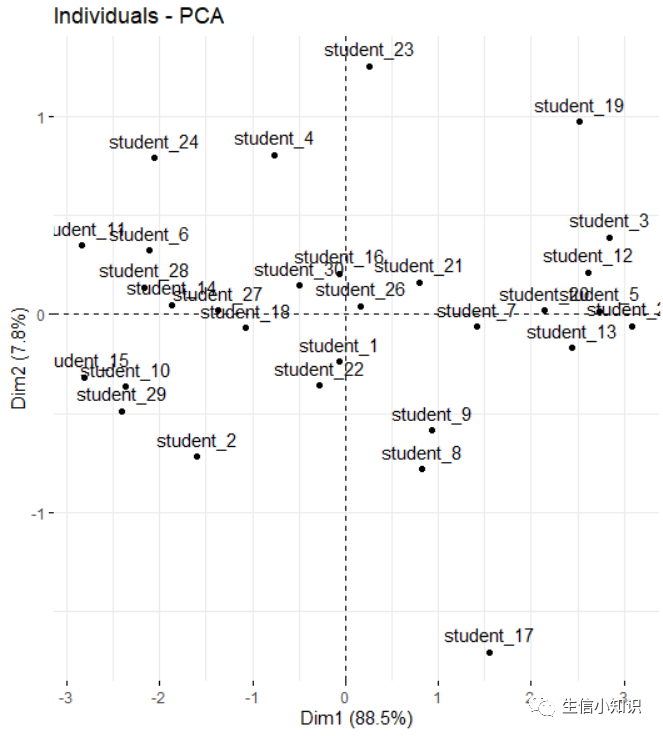
# PCA结果图
fviz_pca_ind(test.pr)
# 手动画散点图
ggplot(as.data.frame(test.pr$scores),aes(Comp.1,Comp.2)) + geom_point()

PCA结果图：

90de45ba9fa46e71270a206632094c21.png

手动画散点图：

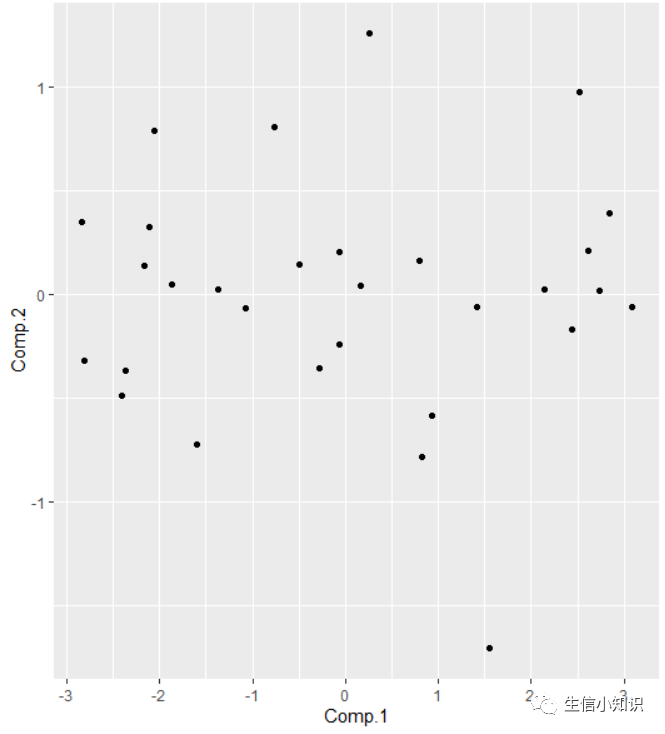
9621bc85c181df5e990b600b74a87e37.png

可以看到，这两者的结果图是一样的！

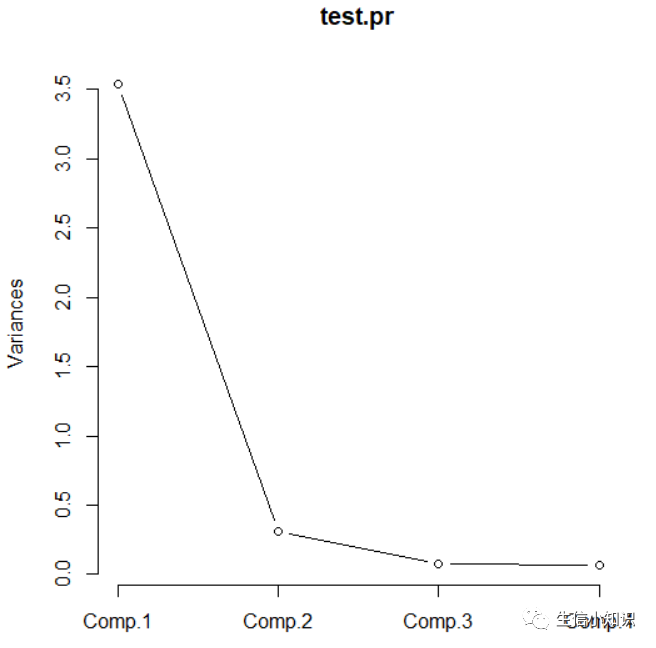
4.画主成分的碎石图并预测
screeplot(test.pr,type="lines")

f995511260b512696db731e7f0f8abe5.png

5.PCA结果绘制

主要用到的函数是fviz_pca_ind，这个函数来自factoextraR包，所以需要先安装&加载才可使用，下面记录下关于这个函数最常用的几个选项：

Usage

fviz_pca_ind(X, axes = c(1, 2), geom = c("point", "text"),
      geom.ind = geom, repel = FALSE, habillage = "none", palette = NULL,
      addEllipses = FALSE, col.ind = "black", fill.ind = "white",
      col.ind.sup = "blue", alpha.ind = 1, select.ind = list(name = NULL, cos2
      = NULL, contrib = NULL), ...)

Arguments
# geom——指定图形上是只显示点，还是同时也显示标签。默认同时显示。
# palette——自行指定颜色
# addEllipses——加95%置信椭圆
# col.ind——每个点的颜色
# legend.title——指定legend的名字

下面看实例：

fviz_pca_ind(test.pr,
             geom.ind = "point",
             col.ind = as.character(c(rep("Normal",15),rep("Tumor",15))),
             palette = c("red", "black"),
             addEllipses = T, 
             legend.title = "Groups")

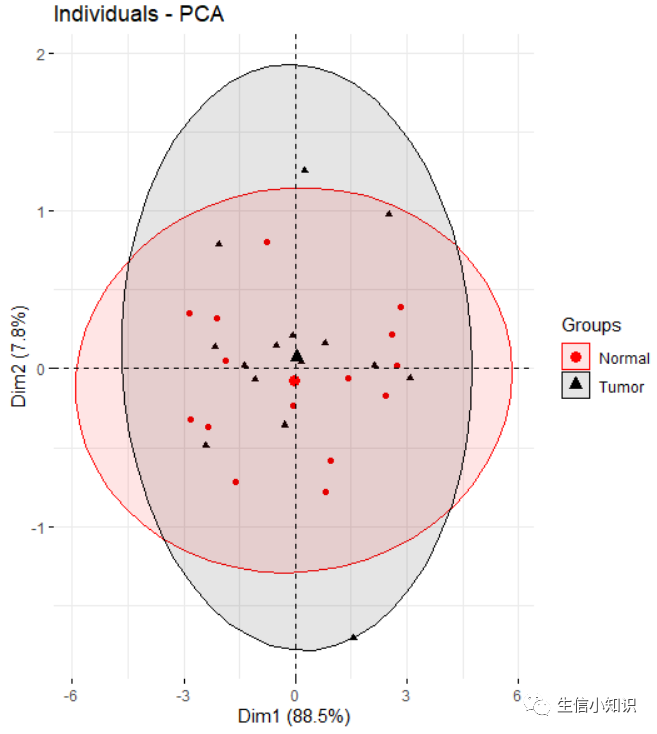
ed3078687403b6f6471fc6b1d08bf7d6.png

是有点丑了，不过也是为了方便理解这个函数每个参数的意义。

后记

稍微整理了下，感觉对PCA怎么画有了更多了解，虽然之前画过，但是都是跑流程，从没有关注具体结果，所以，看似简单，但是却不熟悉。

Liu Baihua
关注
canoco5主成分分析步骤_R语言 PCA主成分分析
weixin_39560029的博客
11-21 1705
微信公众号：生信小知识关注可了解更多的教程及生信知识。问题或建议，请公众号留言;R语言 PCA主成分分析前言统计学背景知识协方差相关系数函数总结实例讲解1.载入原始数据2.作主成分分析3.结果解读4.画主成分的碎石图并预测5.PCA结果绘制后记前言PCA分析大家肯定经常看到，但是你真的懂PCA分析的结果吗？图我也会看，我只是不是很清楚PCA背后输出结果的解读而已。正好看到一篇不错的博客，...
pca 累积方差贡献率公式_特征工程 | PCA降维
weixin_28747937的博客
12-22 1万+
基本思想 主成分分析(PCA)是一种多元统计方法，主要利用降维的思想，在损失很少信息的前提下，把多个变量转化为少数几个互不相关的综合变量，各综合变量即称为主成分。简单来说，主成分与原变量之间应有如下关系：主成分是原变量的线性组合；各主成分之间互不相关；主成分的数目远远小于原变量的数目，且保留了原变量绝大多数信息。 假设有p个变量，分别用表示，随机向量，设随机向量X...
PCA主成分分析与Python应用
最新发布
2403_84646142的博客
05-29 981
主成分分析（Principal Compoent Analysis,PCA）是一种常用的统计方法和降维技术，用于从高维数据中提取重要信息，减少数据的维度，同时尽可能保留数据的关键特征和变化信息。PCA通过将原始数据投射到新的坐标系统中，使得新的坐标轴（主成分）能够最大程度地解释数据的方差在PCA中方差是一个非常重要的概念，它可以帮助我们理解数据的分布和变化情况。方差表示数据点与数据集平均值之间的差异程度。方差越大表明数据点在平均值周围的分布越分散：方差越小，数据点越集中在平均值附近。
PCA利用累计方差贡献率确定主元个数的matlab程序
04-04
PCA主元分析方法中对主元个数确定目前没有非常好的办法，这里提供一个方便的方法来确定主元个数。matlab程序
因子分析累计贡献率_累计方差贡献率和方差贡献率是什么关系SPSS中~~
weixin_39900180的博客
12-20 6954
各方差贡献率相加和等于累计方差贡献率。主成分分析的重点在于解释各变量的总方差，而因子分析则把重点放在解释各变量之间的协方差。主成分分析中不需要有假设，因子分析则需要一些假设。因子分析的假设包括：各个共同因子之间不相关，特殊因子之间也不相关，共同因子和特殊因子之间也不相关。主成分分析中，当给定的协方差矩阵或者相关矩阵的特征值是唯一的时候，主成分一般是独特的；而因子分析中因子不是独特的，可以旋转得到不...
pca 累积方差贡献率公式_主成分分析(PCA)解析 | 统计学习方法 | 数据分析，机器学习，学习历程全记录...
weixin_39603217的博客
12-29 6151
本文包括：主成分分析基本思想主成分分析的数学表达主成分个数规范化变量的总体主成分样本主成分分析1.主成分分析基本思想：在一个数据集中，数据的变量(特征)之间可能存在相关性(互相不独立)，这种相关性增加了分析的难度。在很多模型中，是会假设各个特征之间是独立的，最有代表性的就是朴素贝叶斯模型。为了减少分析难度，提出了主成分分析的方法。主成分分析的最终结果是要用少数不相关的变量来代替相关的变量，这些少数...
pca 累积方差贡献率公式_初识PCA数据降维
weixin_39632327的博客
12-19 3390
PCA要做的事降噪和去冗余，其本质就是对角化协方差矩阵。一.预备知识1.1 协方差分析对于一般的分布，直接代入E(X)之类的就可以计算出来了，但真给你一个具体数值的分布，要计算协方差矩阵，根据这个公式来计算，还真不容易反应过来。网上值得参考的资料也不多，这里用一个例子说明协方差矩阵是怎么计算出来的吧。用matlab计算这个例子z=[1,2;3,6;4,2;5,2]cov(z)ans =2.9167...
pca.zip_pca_pca 排序_主成分分析_主成分分析pca_贡献率
09-20
在标题"pca.zip_pca_pca 排序_主成分分析_主成分分析pca_贡献率"中，我们可以看出这个压缩包文件主要包含了关于PCA的排序和贡献率分析的代码或教程。 PCA的主要目的是将多维数据集转换为少数几个新的变量，这些新...
PCA.zip_PCA函数_pca_主成分_主成分分析
09-20
该函数的使用方法可能是接收一个原始数据矩阵作为输入，然后返回主成分及其对应的载荷（loadings）和贡献率（variance contribution）等信息。 PCA的过程主要包括以下步骤： 1. **标准化**：由于原始数据的各个特征...
PCA.zip_PCA累积_PCA贡献率_pca_pca+lda
09-23
6. **累积贡献率**：累积贡献率是各个主成分所解释的总方差的比例。一般情况下，会选择累积贡献率达到一定阈值（如85%或90%）时的主成分个数，以保证降维后仍能保留大部分信息。 LDA（线性判别分析）则是一种有监督...
PCA.rar_PCA xls_PCA 主成分分析_matlab的主成分分析实例源程序
09-23
累积贡献率是前k个主成分方差之和与所有主成分方差之和的比值。 5. **数据转换**：将原始数据投影到由选中的特征向量构成的空间中，得到新的主成分数据。 在example11_02.m这个源程序中，开发者可能已经实现了以上...
canoco 5 教程.pdf
01-23
canoco是一款生态数据处理软件，这是一款专业性极强的软件，一般的不从事生态研究的人，也不会用到该软件。而在生态研究上，该软件表现得非常专业，它能够对生态学方面的数据进行专业处理，同时涉及的领域也是非常广泛。还可以帮助用户找到研究问题最合适的分析方法，是每个研究人员的好帮手。
canoco5+教程
03-03
生 态 学 软 件 canoco 5 运行INSTALL.EXE安装，使用以下试用许可证： Name: Any Comany: Any License code: c599999 根据系统位数选择Runasdate_x64或者Runasdate_x86，复制到某个软件存放位置 在需要运行的程序填入：C:\Program Files\Canoco5\CanoWin5.exe 时间调整为2010年 在创建桌面快捷方式填入：Canoco 5 然后就可以打开软件了 落尘之木博客：https://www.luochenzhimu.com
Canoco软件的PCA教程
12-01
Canoco软件的PCA教程
基于累计方差贡献率，用MATLAB实现数据降维程序代码
07-17
给定数据模型，用matlab程序代码实现数据的降维，基于方差贡献率来确定最终降维的维数。
canoco教程
12-18
生态软件canoco教程，作者沈会涛，内容：一，群落的排序；二，canoco软件的简介；三，数据的分析。谢谢！
pca 累积方差贡献率公式_主成分分析（PCA）在模型中的运用
weixin_39834281的博客
12-23 1万+
关于主成分分析在模型中的运用主要有以下几个方面：（1）降维；尤其是在面对大量数据时，可以借助PCA方法提取有效的数据成分；其原理，简单的理解就是将众多变量和指标通过一定方法提取出少数几个有代表性的且互相相关性系数较低的变量。（2）处理变量之间多重共线性的问题；（3）确定变量的权重，将多个变量组合成“一个”变量（这在计量经济学论文中常用到，在此不做介绍）。1.主成分在spss中的实现。步骤：分析—降...
因子分析累计贡献率_累计方差贡献率_spss累计方差贡献率_因子分析方差贡献率...
热门推荐
weixin_31995343的博客
01-12 1万+
spss中因子方差贡献率–怎样用SPSS求方差贡献率和方差累计贡献率analyze 下面选择 diemnsion reducation ,再选择factor 因子分析，把你需要计算方差贡献率的变量放到右侧的框里，点击OK，结果里有1张表，就是这些变量的方差贡献率和方差累计贡献率在SPSS中累计方差贡献率和方差贡献率是什么关系方差贡献率是指单个公因子引起的变异占总变异的比例，说明此公因子对因变量的影...
pca主成分分析结果解释_PCA--主成分分析
weixin_39953845的博客
10-22 878
主成分分析（principal component analysis，PCA）是一种无监督学习方法，用来计算主成分理解数据。PCA的主要思想是n个样本值虽然都是存在于p维空间当中，但是并不是所有维度都有同样的价值，PCA致力于寻找少数尽可能有意义的维度来表达数据。而维度是否有意义由所有观测值在每一维度上的离散程度（方差，variance）决定。PCA步骤：假设现在有这么一组数据第一步：数据中心化，...
pca主成分分析方差贡献率代码
04-12
PCA（Principal Component Analysis，主成分分析）是一种常用的降维技术，它通过线性变换将原始数据映射到一个新的特征空间，使得映射后的特征具有最大的方差。方差贡献率是指每个主成分所占总方差的比例，用于衡量主成分对原始数据的解释能力。 下面是一个使用Python进行PCA主成分分析并计算方差贡献率的示例代码： ```python import numpy as np from sklearn.decomposition import PCA # 假设原始数据存储在一个二维数组X中，每行代表一个样本，每列代表一个特征 X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 创建PCA对象，并指定要保留的主成分个数 pca = PCA(n_components=2) # 对原始数据进行PCA降维 X_pca = pca.fit_transform(X) # 计算方差贡献率 variance_ratio = pca.explained_variance_ratio_ print("方差贡献率：", variance_ratio) ``` 在上述代码中，首先导入了必要的库，然后创建了一个PCA对象，并通过`n_components`参数指定要保留的主成分个数。接下来，调用`fit_transform`方法对原始数据进行PCA降维，得到降维后的数据`X_pca`。最后，通过`explained_variance_ratio_`属性获取方差贡献率。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值