（专题七）01 符号对象-矩阵

 符号对象的建立

例如

将数值2转换为符号对象并赋值给t

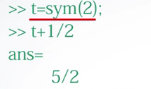
将3分之pi转换为符号对象，再求这个符号对象的正弦值，得到的是一个表达式

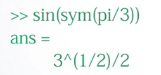
对3分之pi求正弦值，做数值计算，得到的是一个数值

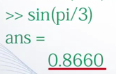
例子：

定义数值变量并赋值

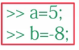
定义符号变量x，y，并赋值，它们分别代表变量a，b

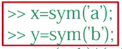
做数值计算

 

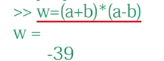
 做符号计算

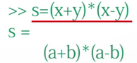
计算符号表达式的值，用eval()函数

syms命令

例如要同时计算四个变量，则

符号对象的四则运算

定义两个符号表达式，并将两个符号表达式相加

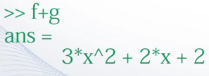
结果是同次项系数相加

 关系运算

例子

建立符号变量x，指定x<0，在指定x的绝对值等于x

因为x<0，是个负数，所以x的绝对值等于负x

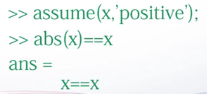
逻辑运算

 

 

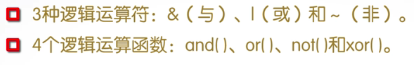
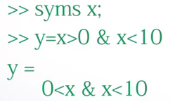
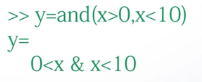
因式分解与展开

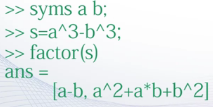
例如使用factor()函数分解因子，12的正因子2，2，3

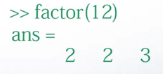
梅森素数的验证问题

梅森数并不一定全为素数

 

 

可见m19不能被分解，故是梅森素数

可见m29能被分解，故不是梅森素数

 可见m31不能被分解，故是梅森素数

注意：素数才不能被因式分解

 求二元一次方程的根

建立符号变量，建立符号表达式

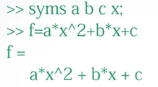
调用提取符号表达式系数函数coeffs(f,x)，将符号表达式f关于x的系数提取出来

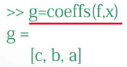
为了得到标准形式，需要将g中的系数反转

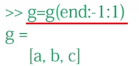
试试看呗----不能

利用多项式求根命令roots，一元二次方程的求根公式就计算出来了

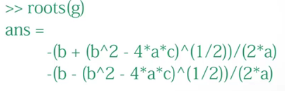
符号运算中变量的确定

例如

建立符号矩阵并简化

调用simplify()函数对矩阵进行化简

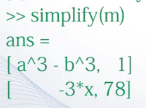
有关矩阵的运算对符号矩阵也适用

 

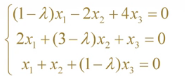
利用来判定

首先建立相应的符号矩阵和相应的系数符号矩阵

然后计算符号矩阵行列式的值

由于A是一个符号矩阵，得到的是一个符号表达式，而不是数值

对行列式的结果进行因式分解

 

转载于:https://www.cnblogs.com/fanglijiao/p/11111291.html