Divide and Conquer.(Merge Sort) by sixleaves

最新推荐文章于 2024-02-25 22:41:53 发布
最新推荐文章于 2024-02-25 22:41:53 发布
阅读量136 收藏
点赞数
CC 4.0 BY-SA版权
原文链接：http://www.cnblogs.com/objectc/p/4722335.html
本文详细介绍了Merge排序算法的动机、伪代码实现及运行时间分析，通过实例展示了如何使用Merge排序对数组进行升序排序，并深入探讨了其复杂度与效率。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

<!doctype html>



algo-C1-Introduction

Merge Sort:一.Motivation and Examplewhy study merge sort?The Sorting ProblemExample:二.Pseudocode:Pseudocode for Merge:Merge Sort Running Time:Running Time of Merge:Running Time of Merge SortRecall:三.AnalysisClaim:Question1:Question2Proof of claim

Merge Sort:

一.Motivation and Example

why study merge sort?

  • Good introduction to divide & conquer
  • Calibrate your preparation
  • Motivates guiding principles for algorithm analysis(worst-case and asymptotic analysis)
  • Analysis generalizes to “Master Method"

The Sorting Problem

Input: array of n numbers, unsorted. (5 4 1 8 7 2 6 3)

Output: same numbers, sorted in increasing order (1 … 8)

Example:

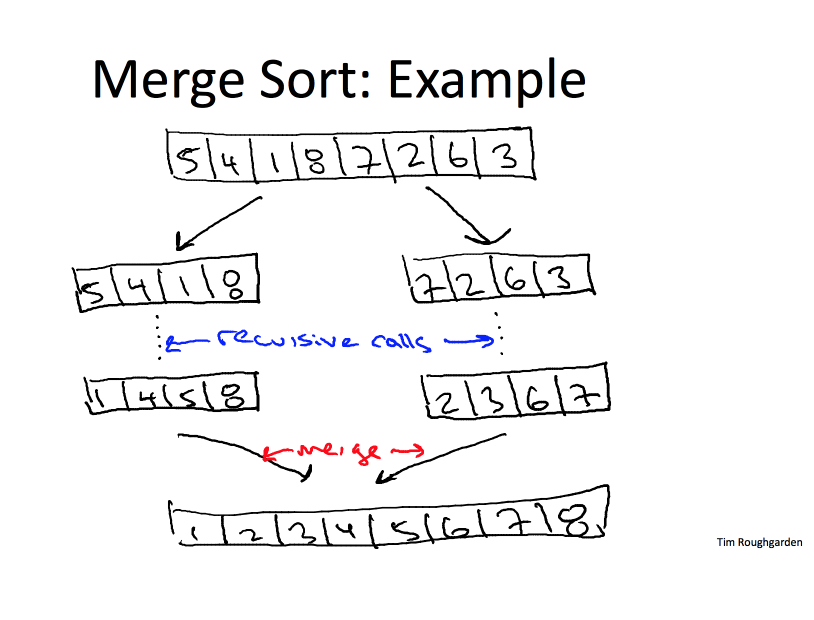
QQ20150811-1

二.Pseudocode:

  • recursively sort 1st half of input array
  • recursively sort 2nd half of input array
  • merge two sorted sublists into one[ ignores base cases]

Pseudocode for Merge:

QQ20150811-2

Merge Sort Running Time:

Key Question: running time of MergeSort on array of n numbers?

[Running time ~ #of mines of code executed ]

Running Time of Merge:

running time of merge on array of m numbers is <= 4m + 2 <= 6m(since m >= 1)

Running Time of Merge Sort

Claim: MergeSort requires <=

6nlog2n+6n

operations for sort n numbers

Recall:

log2n

of times you divide by 2 until you get a number that drops below one

So if you plug in 32 you got to divide five time by two get down to one.

三.Analysis

Claim:

For every Input array of n numbers, Merge Sort produces a sorted output array and uses at most 6nlog_2n + 6n operations.

Proof of calim (assuming n = power of 2):

Question1:

how many levels does this recursion tree have.===>

beacause: {level0, level1……. level(log2n)} === > (log_2n - 0) + 1 ===>

log2n+1

Question2

at each level j = 0,1 ,2 , log_2n, there are 2^j subproblems, each of size n / 2^j.

第二个的原因很简单, 这颗递归树的第j层的子问题有 2^j 个, 例如第0层是1个, 第1层是两个, 由此类推, 所以每个的大小都是n / 2^j.

Proof of claim

第j层总的合并程序中所含有的指令次数是 <= 2 ^j * 6(n / 2^j) = 6n.也就是所每一层的合并程序内部所做的指令次数都是固定的, 为6n次, 所以对于这课共有log2n + 1个层的数, 总的操作次数为6n( log2n + 1) = 6nlog_2n + 6n.

转载于:https://www.cnblogs.com/objectc/p/4722335.html

Divide-and-conquer思想在Merge Sort & quick sort的应用
Huangkaihong的博客
05-11 403
Divide-and-conquer思想在Merge Sort & quick sort的应用 分而治之的思想指的是： 把原问题（problem）拆分成一个个相似的小问题（subproblem）， 然后用同样的方法对这些小问题进行处理， 最后再合并这些小问题的答案得到原问题的答案 一： 归并排序（merge sort）中运用了分而治之（divide-and-conquer）的思想. 举个例子：divide-and-conquer application to merge sorting: 图中
算法详解（卷一）——MergeSort算法（Python）
没同学的博客
04-17 1161
算法详解阅读笔记使用书籍——算法详解算法详解（卷一）内容概述MergeSort算法（归并排序）问题描述问题分析代码写在最后 使用书籍——算法详解 出于转统计学的缘故，需要良好的算法基础，所以在朋友推荐下，选择《算法详解》系列图书入门，全套4卷。这套书是Tim Roughgarden教授在其在线算法课程的基础之上编写的，在线课程Coursera上可以找到。（系列书籍上的所有算法用伪代码描述，代码部分...
Lecture 10: Divide and conquer methods, merge sort, exceptions
sunner008的专栏
09-25 268
# Lecture 10 fall 2008 def merge(left,right): result = [] i,j = 0, 0 while i < len(left) and j < len(right): if left[i] <= right[j]: result.append(left[i])
Algorithms Review: Divide and Conquer(Binary Search & Merge Sort)
07-15 490
#include #include #include #include #include using namespace::std; class DivideAndConquer { public: int binarySearch(int target, int* inputArray, int size) { if(size < 1) { cout<<"error"<<e
归并排序详解merge sort python代码实现
Ying_ying_123的博客
02-28 980
归并排序中采用的分而治之(divide-and-conquer)的思想. 把大问题(原问题)拆成一个一个相似的小问题，然后对这些小问题采用相同的方法进行处理，再最后合并各个小问题的答案，最后就得到了原问题的答案。 在讲怎么把原问题分解成一个一个小问题之前，我们需要一个合并函数来将两个无序的序列合并成一个有序的序列 1 现在我们手里有三个序列， 一个是未排序的序列A: [19, 21, 3, 1, ...
Recursion / Divide and Conquer - Merge Sort
qq_40688707的博客
08-18 235
Merge Sort Write a program of a Merge Sort algorithm implemented by the following pseudocode. You should also report the number of comparisons in the Merge function. Merge(A, left, mid, right) n1...
算法学习笔记--5.merge sort & divide-and-conquer
丰伟磊的博客
08-10 698
归并排序； 分而治之。
divide and conquer 2.zip_algorithm_conquer_divide and conquer
09-15
分治法（Divide and Conquer）是计算机科学中一种重要的算法思想，它的核心理念在于将一个复杂的问题分解成若干个规模较小、相互独立、与原问题形式相同的子问题，然后分别解决这些子问题，最后将子问题的解组合起来...
python-divide-and-conquer.rar
05-28
在计算机科学中，分治（Divide and Conquer）是一种重要的算法设计策略，它将一个复杂的问题分解成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这种策略在...
DivideandConquer技术专题培训.pptx
05-25
Divide-and-Conquer（分治法）是一种重要的算法设计范式，其核心思想是将一个难以直接解决的大问题划分成若干个小问题，递归解决各个小问题，然后合并这些小问题的解以得到原问题的解。这种方法在多个领域，特别是...
merge-and-count.zip_merge and count
09-20
在计算机科学领域，算法的设计和分析是核心部分，而“分治法”（Divide and Conquer）作为一种经典策略，广泛应用于解决复杂问题。"merge-and-count"这个任务，正是基于这一策略的实践，旨在实现一种“sort and ...
【数据结构与算法】(22)高级数据结构与算法设计之 Divide and Conquer 分治法 代码示例与详细讲解
02-25 830
分治思想将大问题划分为两个到多个子问题子问题可以继续拆分成更小的子问题，直到能够简单求解如有必要，将子问题的解进行合并，得到原始问题的解之前学过的一些经典分而治之的例子二分查找快速排序归并排序合并K个排序链表 - LeetCode 23。
mmexport1755325166750.mp4
08-16
mmexport1755325166750.mp4
Go语言教程&案例&相关项目资源
08-16
Go语言教程&案例&相关项目资源
基于应力的多轴疲劳分析应用程序.zip
08-16
1.版本：matlab2014a/2019b/2024b 2.附赠案例数据可直接运行。 3.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
### 生物质炉具现场测试污染物排放特征及减排效果评估
08-16
内容概要：该研究通过在黑龙江省某示范村进行24小时实地测试，比较了燃煤炉具与自动/手动进料生物质炉具的污染物排放特征。结果显示，生物质炉具相比燃煤炉具显著降低了PM2.5、CO和SO2的排放（自动进料分别降低41.2%、54.3%、40.0%；手动进料降低35.3%、22.1%、20.0%），但NOx排放未降低甚至有所增加。研究还发现，经济性和便利性是影响生物质炉具推广的重要因素。该研究不仅提供了实际排放数据支持，还通过Python代码详细复现了排放特征比较、减排效果计算和结果可视化，进一步探讨了燃料性质、动态排放特征、碳平衡计算以及政策建议。 适合人群：从事环境科学研究的学者、政府环保部门工作人员、能源政策制定者、关注农村能源转型的社会人士。 使用场景及目标：①评估生物质炉具在农村地区的推广潜力；②为政策制定者提供科学依据，优化补贴政策；③帮助研究人员深入了解生物质炉具的排放特征和技术改进方向；④为企业研发更高效的生物质炉具提供参考。 其他说明：该研究通过大量数据分析和模拟，揭示了生物质炉具在实际应用中的优点和挑战，特别是NOx排放增加的问题。研究还提出了多项具体的技术改进方向和政策建议，如优化进料方式、提高热效率、建设本地颗粒厂等，为生物质炉具的广泛推广提供了可行路径。此外，研究还开发了一个智能政策建议生成系统，可以根据不同地区的特征定制化生成政策建议，为农村能源转型提供了有力支持。
汽车嵌入式开发资料：NXP Cloud Lab 恩智浦云实验室
08-16
汽车嵌入式开发资料：NXP Cloud Lab 恩智浦云实验室
A153基于springboot+vue的公交智能化系统（LW文档+完整前后端代码+sql脚本+开发文档+全套软件）
08-16
项目介绍 公交智能化系统可以将功能划分为用户和管理员功能 用户关键功能包含用户注册登陆、科目任务、公交线路、公交站点、公交信息、周边服务、公交动态、天气、我的等有关功能. 管理员的权限是最高的，可以对系统所在功能进行査看，修改和删除。管理员进入系统主页面，主要功能包括对系统首页、用户管理、线路管理、车次管理、公交线路管理、公交站点管理、公交信息管理、周边服务管理、公交动态管理、系统管理、我的信息等进行操作。 项目已获导师指导并通过的高分毕业设计项目，可作为课程设计和期末大作业，下载即用无需修改，项目完整确保可以运行。 包含：项目源码、数据库脚本、软件工具等，该项目可以作为毕设、课程设计使用，前后端代码都在里面。 该系统功能完善、界面美观、操作简单、功能齐全、管理便捷，具有很高的实际应用价值。 项目都经过严格调试，确保可以运行！可以放心下载 视频演示地址： 链接: https://pan.baidu.com/s/1gsV1hPJzQtIWjGjpXsce8A?pwd=9nyn 提取码: 9nyn
excel有选择的批量删除单元格数据.doc
最新发布
08-17
excel有选择的批量删除单元格数据.doc
divide and conquer时间复杂度
12-31
### 分治算法的时间复杂度 分治算法是一种重要的算法设计技术，其核心在于将一个问题分解成多个较小规模的相同问题，分别求解后再合并各个子问题的结果得到原始问题的答案。对于这类算法而言，时间复杂度主要取决于三个因素： - **分解操作的成本**：即将原问题划分为更小子问题所需的工作量。 - **解决各子问题所需的总成本**：这通常是递归调用本身的时间开销。 - **组合子问题解决方案的成本**：即如何有效地把所有子问题的解答汇总起来形成最终答案。 #### 计算方法 为了计算分治算法的时间复杂度，可以利用主定理（Master Theorem），它提供了一种简便的方法来估计形如 \(T(n)=aT(\frac{n}{b})+f(n)\) 的递推关系式的渐近界[^3]。这里， - \(n\) 表示输入大小； - \(a \geq 1\) 和 \(b > 1\) 是常数； - \(f(n)\) 描述了除递归外其他部分工作量的增长速度。 当应用到具体的例子时，比如快速排序，如果每次都能均匀分割，则有 \(a=2\),\(b=2\),而额外处理（比较和交换元素）大致线性增长，因此 \(f(n)=O(n)\)，从而得出平均情况下快速排序的时间复杂度为 \(O(n\log n)\)[^4]。 #### 示例 考虑经典的归并排序作为实例展示分治算法及其时间复杂度分析过程: ```java public class MergeSort { public static void merge(int[] array, int left, int mid, int right){ // 合并两个已排序序列... } public static void sort(int[] array, int left, int right){ if (left < right){ int mid = (left + right)/2; // 对左半边进行递归排序 sort(array, left, mid); // 对右半边进行递归排序 sort(array, mid+1, right); // 将两部分有序数组合并在一起 merge(array, left, mid, right); } } } ``` 在这个实现中，`sort()` 函数负责递归地拆分子数组直到不能再分为止，之后再由 `merge()` 来完成实际的数据整理任务。由于每层递归都会使待处理区间减半，并且每一层都需要遍历整个列表来进行合并操作，故此算法的整体时间复杂度同样遵循 \(O(n\log n)\) 的规律。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值