1. 生成树
一个连通图的生成树是一个极小连通子图,它包含图中的全部顶点,但只有构成一棵树的n-1条边。
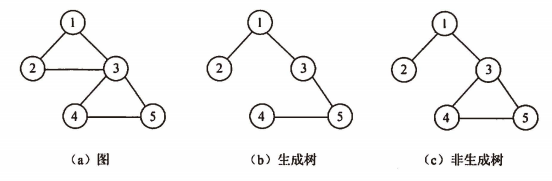
对于有n个顶点的连通图,至少有n-1条边,而生成树中恰好有n-1条边,所以连通图的生成树是该图的极小连通子图。若在图的生成树中任意加一条边,则必然形成回路。
2. 最小生成树
对于连通网来说,边是带权值的,生成树的各边也带权值,因此把生成树各边的权值总和称为生成树的权,把权值最小的生成树称为最小生成树。
a. 普里姆算法
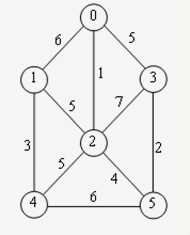 →
→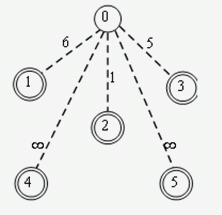 →
→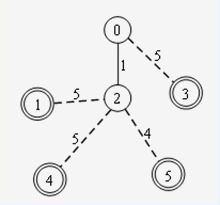 →
→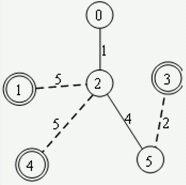 →
→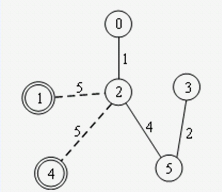 →
→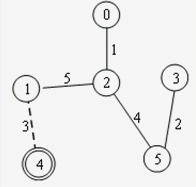 →
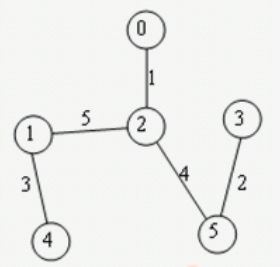
→
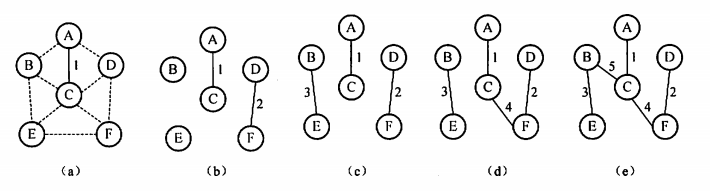
b. 克鲁斯卡尔算法
1. 生成树
一个连通图的生成树是一个极小连通子图,它包含图中的全部顶点,但只有构成一棵树的n-1条边。

对于有n个顶点的连通图,至少有n-1条边,而生成树中恰好有n-1条边,所以连通图的生成树是该图的极小连通子图。若在图的生成树中任意加一条边,则必然形成回路。
2. 最小生成树
对于连通网来说,边是带权值的,生成树的各边也带权值,因此把生成树各边的权值总和称为生成树的权,把权值最小的生成树称为最小生成树。
a. 普里姆算法
 →
→ →
→ →
→ →
→ →
→ →
→
b. 克鲁斯卡尔算法

转载于:https://www.cnblogs.com/ImaY/p/4367688.html

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


